Prev. Section Next Section

Mecánica FI2001

Trabajo y energía

Para ciertos ejercicios, la conservación de la energía mecánica nos permite resolver el problema de una forma mucho más simple que usando segunda Ley de Newton.

La fórmula clave con la que resolveremos los problemas es la diferencia de la energía mecánica

\begin{gather}\label{eq:formula-maestra} E_B-E_A=W_{AB}^{\textnormal{NC}}\\ \Leftrightarrow K_B + U_B - K_A - U_A=W_{AB}^{\textnormal{NC}} \label{eq:deltaEW} \end{gather}

Para utilizar esta ecuación debemos seguir $10$ pasos

  1. Primer paso: Hacerse una idea de cómo se mueve la partícula
  2. Segundo paso: Identificar las fuerzas que están actuando sobre la partícula
  3. Tercer paso: Elegir un sistema de coordenadas adecuado
  4. Cuarto paso: Expresar matemáticamente las fuerzas en el sist. de coord. elegido
  5. Quinto paso: Distinguir cuáles fuerzas son conservativas y cuáles son no conservativas
  6. Sexto paso: Calcular el potencial asociado a las fuerzas conservativas
  7. Séptimo paso: Calcular el trabajo asociado a las fuerzas no conservativas
  8. Octavo paso: Expresar la energía cinética con el sist. de coord. elegido
  9. Noveno paso: Reemplazar todo en (\ref{eq:deltaEW})
  10. Décimo paso: Calcular las cantidades que nos piden en el problema

Para aterrizar algunos de estos pasos, veremos el siguiente Ejemplo:

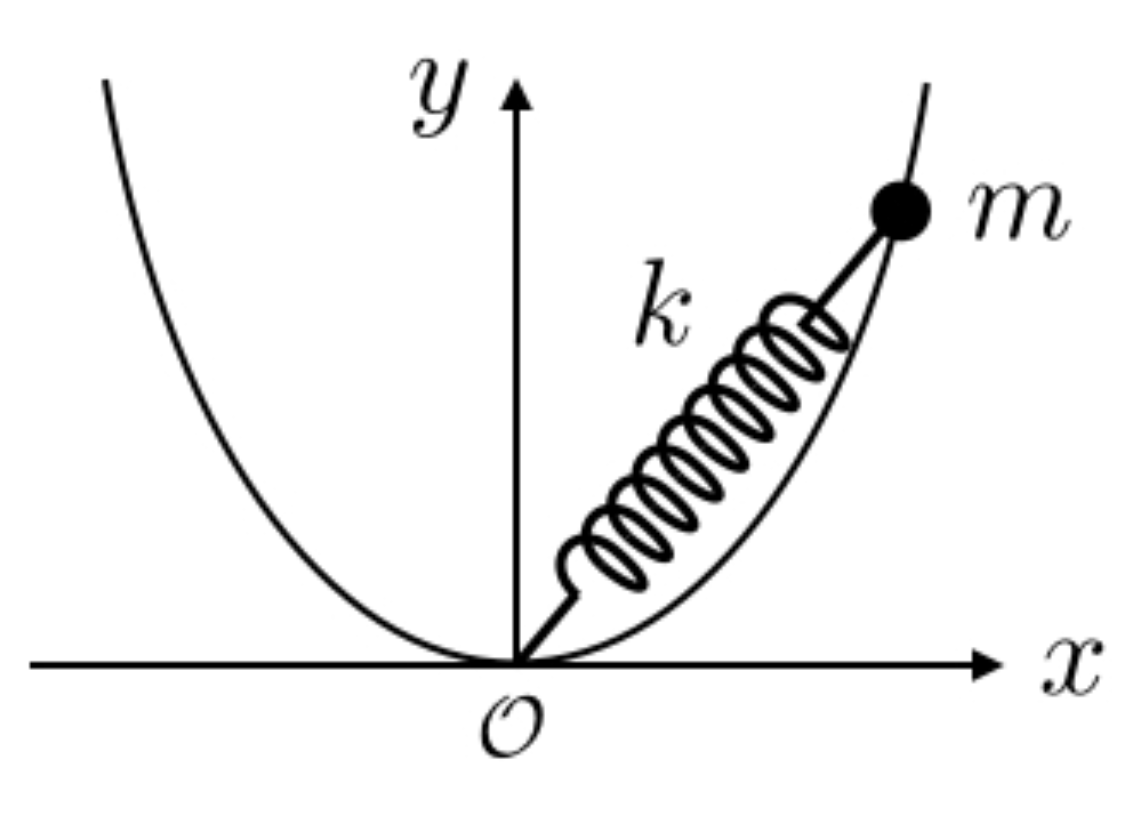
Description of the image
Fig.1 Problema de ejemplo

Donde un anillo de masa $m$ puede deslizar sin roce por un alambre con forma dada por $y=x^2/x_0$. El anillo está unido a un resorte ideal de constante $k$, largo natural 0 ($l_0=0$), y sujeto al punto $\mathcal{O}$. Además de la fuerza del resorte $\vec{F}_R$ y de la fuerza ejercida por el alambre $\vec{F}_A$, sobre el anillo acúa una fuerza externa

\begin{equation*} \vec{F}_E=\frac{k}{x_0}\left(xy\hat{i}+\frac{3x_0}{4}y\hat{j}\right)\,. \end{equation*}

  1. Imaginar el movimiento

Al igual que en la sección de Dinámica, tenemos que tener al menos una idea de cómo se movería la partícula y donde se encontraría en distintos tiempos. Por ejemplo, en algunos problemas tenemos fuerzas de restricción que obligan a la partícula a seguir ciertas trayectorias bien definidas.

En nuestro Ejemplo, es claro que sin importar el valor de las fuerzas $\vec{F}_R$ y $\vec{F}_E$, la partícula siempre se moverá siguiendo la parábola $y=x^2/x_0$, gracias a la fuerza normal del alambre. Además, por cómo se comporta un resorte, podemos hacer el guess que la partícula irá en un movimiento de vaivén, donde se detendría por un momento en las distancias más lejanas.

  1. Identificar las fuerzas

Hay que hacer un listado de todas las fuerzas que se ejercen sobre la partícula, para poder describirlas matemáticamente, y luego clasificarlas en conservativas y no conservativas.

En nuestro Ejemplo tenemos 3 fuerzas:

  1. Sistema de coordenadas

La elección del sistema de coordenadas que utilizaremos depende de dos cosas: (1) la expresión de las fuerzas implicadas y (2) el movimiento de la partícula. No siempre encontraremos "el sistema de coordeandas perfecto", por lo que tienen que equilibrar entre que sea fácil trabajar con las fuerzas y que sea fácil describir el movimiento de la partícula.

En nuestro Ejemplo nos dan en coordenadas cartesianas la fuerza $\vec{F}_E$ y el movimiento de la partícula ($y=x^2/x_0$), por lo que, aunque sea fácil describir la fuerza del resorte en esféricas, trabajaremos con cartesianas para tener que hacer la menor cantidad de descomposiciones posible.

  1. Expresar las fuerzas

Para poder utilizar \eqref{eq:formula-maestra}, tenemos que calcular las energías potenciales en distintos puntos. Para eso, primero debemos expresar matemáticamente las fuerzas que idenfitifcamos en el Segundo paso.

En nuestro ejemplo $\vec{F}_E$ ya está descrito matemáticamente, mientras que la fuerza del resorte sería

\begin{equation*} \begin{aligned} \vec{F}_R&=-k\sqrt{x^2+y^2}\hat{r}\\ &=-k\sqrt{x^2+\frac{x^4}{x_0^2}}\hat{r} \end{aligned} \end{equation*}

donde, por enunciado, el largo natural es nulo.

Notamos que para $\vec{F}_R$ no descompusimos $\hat{r}$ en cartesianas, ya que ocuparemos su potencial, que es una cantidad escalar, así que nos podemos olvidar de los vectores. Esta es una de las gracias de trabajar con energía en vez de segunda Ley de Newton, ya que la primera es puramente escalar, por lo que no hay que complicarse con descomposición de vectores.

  1. Clasificar las fuerzas

Ya habiendo hecho una lista de todas las fuerzas actuando sobre la partícula, y también haberlas descrito matemáticamente, hay que saber cuáles son conservativas y cuáles no conservativas.

De forma general, una fuerza es conservativa si su rotor es 0

\begin{equation*} \nabla\times \vec{F}=0. \end{equation*}

Si cumple esta condición, entonces podemos calcular su potencial asociado (ver Sexto paso).

Sin embargo, de antemano podemos saber si una fuerza es conservativa y poder ahorrarnos el cálculo del rotor. Casos típicos de fuerzas conservativas son las radiales, $\vec{F}(\vec{r})=F(r)\hat{r}$, donde pueden demostrar que para cualquier expresión de $F(r)$, el rotor de esta fuerza es nulo.

Adicionalmente, hay ciertas fuerzas típicas que tienen un potencial asociado conocido, como las que se muestran en el Sexto paso, por lo que para estas tampoco es necesario demostrar que son conservativas.

De tener solo fuerzas conservativas nos evitamos tener que calcular trabajos, ya que tendríamos

\begin{equation*} E_A=E_B. \end{equation*}

Aunque, ojo que la conservación de energía mecánica no implica que las fuerzas implicadas no hagan trabajo, ya que las fuerzas conservativas también pueden ejercer trabajo, que vendría dado por la diferencia de la energía potencial evaluada en distintos puntos.

En cambio, las fuerzas no conservativas hacen que el sistema pierda energía, por lo que tendremos que calcular su trabajo asociado para obtener la diferencia de energía mecánica (ver Séptimo paso).

En nuestro Ejemplo:

  1. Calcular los potenciales

A las fuerzas conservativas hay que calcularles su potencial asociado. Para una fuerza conservativa cualquiera ocupamos la fórmula:

\begin{equation}\label{eq:potencial} U(r)=-\int^r \vec{F}(\vec{r}^{\, \prime})\cdot \text{d}\vec{r}^{\, \prime}\,, \end{equation}

donde no importa dónde pongamos el punto inicial, digamos $\vec{r}_0$, ya que en física solo medimos diferencias de potencial, o sea, nos quedamos solo con la primitiva e ignoramos la constante de integración.

Sin embargo, como les mencioné, hay fuerzas conservativas que se repiten en los ejercicios y sus potenciales son conocidos, y podemos utilizarlos sin tener calcular con (\ref{eq:potencial}). Algunos potenciales conocidos son:

  • Elástica:
    \begin{equation*} U(r) = \frac{1}{2}k(r-l_0)^2 \end{equation*}
  • Gravitacional:
    \begin{equation*} U(r)= -G\frac{m_1m_2}{r} \end{equation*}
  • Gravitacional:
    \begin{equation*} U(z)= mgz \end{equation*}
  • Coulomb:
    \begin{equation*} U(r)= k\frac{q_1q_2}{r} \end{equation*}

En nuestro Ejemplo, la única fuerza conservativa es $\vec{F}_R$ y su potencial sería $U(r)=kr^2/2$, ya que $l_0=0$.

  1. Calcular los trabajos

Recuerden que tenemos la relación

\begin{equation}\label{eq:diferencia-energia} E_B-E_A=W^{\textnormal{NC}}_{AB}\,, \end{equation}

donde $W^{\textnormal{NC}}_{AB}$ es el trabajo realizado por todas las fuerzas no conservativas desde el el punto $\vec{r}_A$ al punto $\vec{r}_B$. Entonces, debemos calcular el trabajo realizado por cada fuerza no conservativa y sumar cada una de estas contribuciones:

\begin{equation*} W^{\textnormal{NC}}_{AB}=\int_{\vec{r}_A}^{\vec{r}_B}\vec{F}^{\textnormal{NC}}_{\textnormal{tot}}\cdot \text{d}\vec{r}\,. \end{equation*}

Ahora, en un problema nos pueden pedir explícitamente que calculemos el trabajo realizado por una fuerza conservativa $\vec{F}^{\textnormal{C}}$, y podemos hacerlo con la fórmula usual del trabajo

\begin{equation*} W_{AB}=\int_{\vec{r}_A}^{\vec{r}_B}\vec{F}(\vec{r}^{\,\prime})\cdot \text{d}\vec{r}^{\,\prime}, \end{equation*}

o podemos hacer uso de la relación, válida solo para fuerzas conservativas:

\begin{equation}\label{eq:trabajo-conservativas} \begin{aligned} W^{\textnormal{C}}_{AB}&=\int_{\vec{r}_A}^{\vec{r}_B}\vec{F}^{\textnormal{C}}(\vec{r}^{\,\prime})\cdot d\vec{r}^{\,\prime}\\ &=U(r_A)-U(r_B)\,, \end{aligned} \end{equation}

donde $\vec{F}^{\textnormal{C}}=-\nabla U$, o sea, $U$ es el potencial asociado.

Se pueden preguntar por qué calcular el trabajo de las fuerzas conservativas si es que no aparece en (\ref{eq:diferencia-energia}). Esto es porque el trabajo total esta dado por

\begin{equation*} W_{AB}^{\textnormal{tot}}=W^{\textnormal{C}}_{AB}+W^{\textnormal{NC}}_{AB} \end{equation*}

y a su vez este trabajo total cumple la relación

\begin{equation*} \begin{aligned} W_{AB}^{\textnormal{tot}}&=\int_{\vec{r}_A}^{\vec{r}_B}\vec{F}^{\textnormal{tot}}(\vec{r}^{\,\prime})\cdot \text{d}\vec{r}^{\,\prime}\\& =K(r_B) - K(r_A), \end{aligned} \end{equation*}

o sea, nos da la diferencia de la energía cinética, con lo que podemos hacer cosillas...

  1. Energía cinética

La energía cinética de una partícula, de forma general, se expresa como

\begin{equation} K=\frac{1}{2}m|\vec{v}|^2, \end{equation}

y en coordenadas cartesianas, cilíndricas y esféricas sería:

\begin{align*} K=& \, \frac{1}{2}m\left(\dot{x}^2 + \dot{y}^2 + \dot{z}^2\right)\\ =& \, \frac{1}{2}m\left({\dot{\rho}}^2 + \rho^2{\dot{\phi}}^2 + {\dot{z}}^2\right)\\ =& \, \frac{1}{2}m\left({\dot{r}}^2 + r^2{\dot{\theta}}^2 + r^2{\dot{\phi}}^2\sin^2\theta\right) \,. \end{align*}

Cuando tenemos fuerzas de restricción (normales o tensiones), algunos de estos términos van a ser 0 para todo tiempo. Por ejemplo, en un problema que estemos usando cilíndricas y tenemos una distancia radial y altura constante para todo tiempo , entonces $\dot{\rho}=\dot{z}=0\Rightarrow K=m\rho^2\dot{\phi}^2/2$.

También, la energía cinética en \eqref{eq:formula-maestra} está evaluada en dos instancias particulares, cuando la partícula se encuentra en $A$ y luego en $B$. Dependiendo de estos puntos, es que algunas componentes de la rapidez puede ser $0$.

  1. Reemplazar

Después de todos estos pasos deberían tener: (1) El potencial asociado a cada fuerza conservativa, (2) el trabajo hecho por las fuerzas no conservativas, y (3) la expresión de la energía cinética. Esto deben reemplazarlo en (\ref{eq:deltaEW}) evaluando cada energía en su posición (o tiempo) correspondiente: $A$ y $B$.

  1. Calcular lo que nos piden

Noten que (\ref{eq:deltaEW}) es solo una ecuación, así que, después de haber evaluado cada energía en su posición (o tiempo) correspondiente utilizando la información del enunciado y condiciones físicas, solo deben quedar con 1 incógnita, que es el término que queremos calcular.

Lo más común es utilizar $E_A$ como la energía en el tiempo inicial, ya que en muchos casos nos dan las condiciones iniciales de la partícula (su posición y velocidad inicial), por lo que podríamos calcular cuánto vale la energía mecánica inicial. Luego, el punto $\vec{r}_B$ en el tiempo $t_E$ es dónde nos interesa calcular cosas, por ejemplo, podemos conocer la posición (y así la energía potencial $U_B$) y con esto despejar la velocidad (contenida en $K_B$), y viceversa.

En resumen, este paso es simplemente despejar una incógnita.

  • Material Complementario

Si deseas profundizar más en este tópico o ver cómo se resuelven problemas concretos, te invito a revisar los siguientes enlaces:

Prev. Section Next Section