Notes | Lagrangiano

Hasta ahora hemos estado abordando los problemas del curso con mecánica Newtoniana. La mecánica lagrangiana nos permite encontrar las ecuaciones de movimiento escalares sin la necesidad de descomponer fuerzas y todas las vueltas que nos dábamos con mecánica newtoniana debido a que se definía de forma vectorial.

La ecuación maestra de esta unidad será la ecuación de Euler-Lagrange

\begin{equation}\label{eq:E-L} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right)=\frac{\partial L}{\partial q_i}\,, \end{equation}

donde $q_i$ es la coordenada $i$-ésima y $L$ es el lagrangiano de nuestro problema y está dado por

\begin{equation}\label{eq:L} L=K(\dot{q})-U(q)\,, \end{equation}

con $K$ y $U$ la energía cinética y potencial total del sistema (podemos tener más de una partícula).

Para resolver los problemas usando mecánica lagrangiana, en general seguimos los siguientes pasos

Primer paso: Hacerse una idea de cómo se mueve la(s) partícula(s) y elegir un sistema de coordenadas adecuado
Segundo paso: Identificar las fuerzas que están actuando sobre las partículas y clasificarlas en: conservativas o de restricción
Tercero paso: Calcular el potencial asociado a cada fuerza conservativa y expresar la energía potencial total del sistema
Cuarto paso: Expresar la energía cinética total sistema
Quinto paso: Relacionar entre sí las distintas coordenadas $q_i$ según el movimiento de las partículas
Sexto paso: Expresar el lagrangiano del sistema (\ref{eq:L}) y calcular la ecuación de Euler-Lagrange (\ref{eq:E-L}) para cada coordenada $q_i$
Séptimo paso: Calcular lo que nos pidan en el enunciado

Para aterrizar algunos de estos pasos, veremos el siguiente Ejemplo:

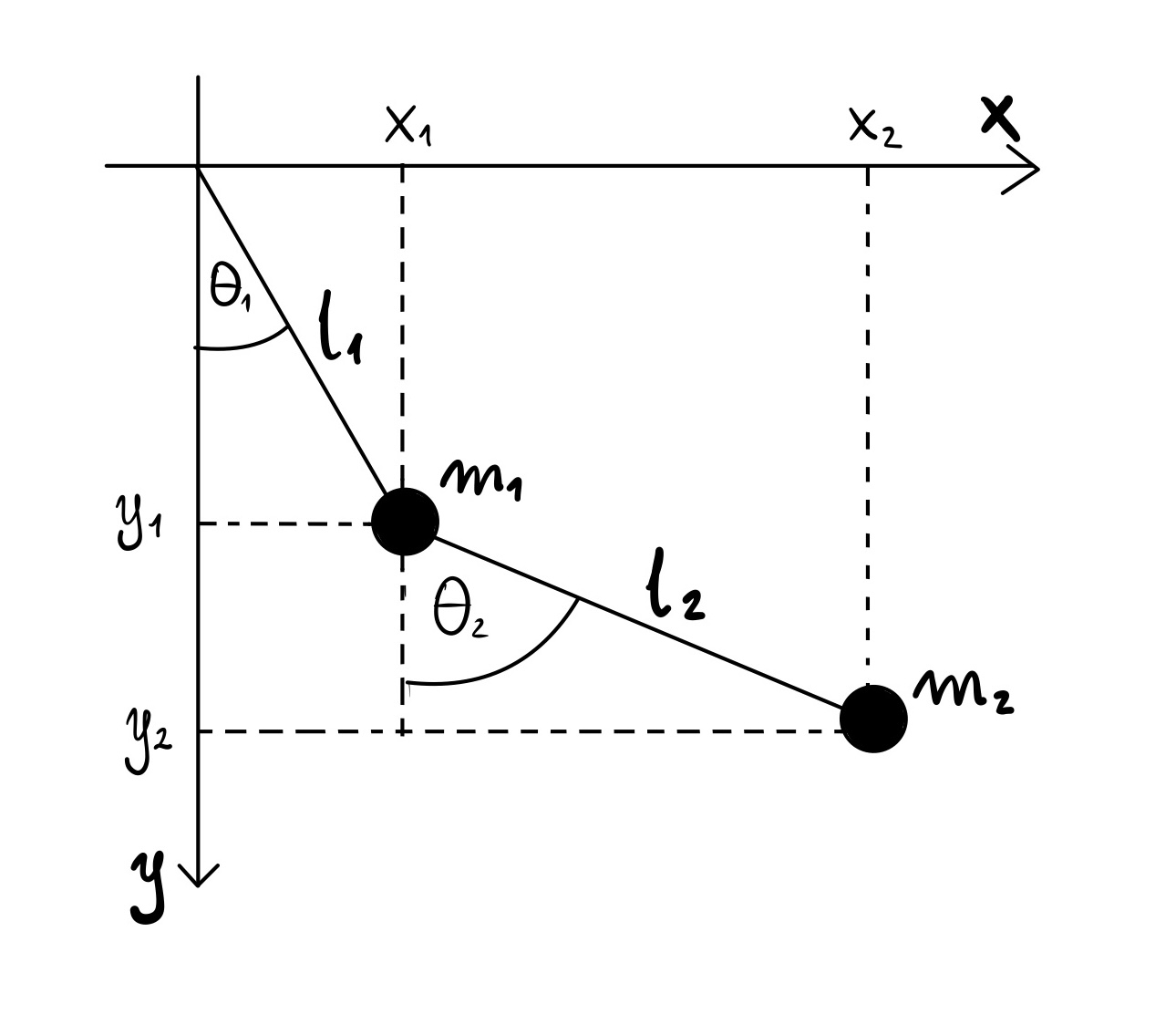
Description of the image — Fig.1 Problema de ejemplo

Considere un péndulo doble como el mostrado en la figura en presencia de gravedad.

¿Cuántos grados de libertad tiene el problema?
Calcule el lagrangiano del problema
Calcule las dos ecuaciones de movimiento
Calcule la frecuencia de pequeñas oscilaciones y los modos normales [Subsección]

Primer paso: Coordenadas y grados de libertad

Debido a que los ejes de un sistema de coordeandas cartesiano son independientes de la posición de las partículas (a diferencia de esféricas y cilíndricas), en muchos problemas que usemos lagrangiano será más conveniente ocupar este sistema de coordenadas debido a que trabajaremos con más de una partícula.

Entonces, en este problema aunque las partículas sigan movimientos curvos, ocuparemos cartesianas. Debemos definir las coordeandas de nuestras partículas como:

\begin{equation*} \vec{r}_1=(x_1,\,y_1)\,, \qquad \vec{r}_2=(x_2,\, y_2) \end{equation*}

donde definimos el eje $\hat{y}$ apuntando hacia abajo y $\hat{x}$ hacia la derecha (con origen en la parte de arriba).

Algo importante que tenemos que preguntarnos inicialmente es la cantidad de grados de libertad del problema, que es la cantidad mínima de variables que necesitamos para describir la posición de la(s) partícula(s).

En general, podemos seguir la siguiente regla para el caso de una partícula moviéndose en:

Una línea (curva o recta): un grado de libertad
Una superficie (curva o plana): dos grados de libertad
Un volumen: tres grados de libertad

En el caso con $n$ partículas sería lo mismo, pero multiplicado por $n$, a menos que hayan fuerzas de restricción entre ambas partículas. La cantidad de grados de libertad nos dice la cantidad de ecs. de movmiento que obtendremos.

En nuestro Ejemplo notamos que nos basta con conocer $\theta_1$ y $\theta_2$ para conocer la posición de ambas partículas, por lo que el problema tiene dos grados de libertad, así que al final deberíamos tener dos ecuaciones de movimiento.

Segundo paso: Fuerzas

Para ocupar lagrangiano (por lo menos en este curso) no podemos tener fuerzas disipativas (como la fuerza de roce cinético o viscoso).

Una de las gracias de la mecánica lagrangiana es que nos olvidamos de encontrar expresiones de las fuerzas de restricción (a diferencia de cuando ocupábamos mecánica newtoniana), que son las fuerzas que fijan el movimiento de una partícula o fijan el movimiento entre partículas. Las fuerzas de restricción comúnes son: fuerza normal, fuerza peso, fuerza de barras entre partículas.

Viendo nuestro Ejemplo, sobre ambas partículas está actuando la fuerza peso y fuerzas de tensión o empuje ejercidas por las barras que las unen. Estas fuerzas las clasificamos como:

Fuerza peso: Conservativa
Fuerzas de las barras: De restricción

Tercer paso: Energía potencial

Ya habiendo clasificado las fuerzas, debemos calcular el potencial de nuestras fuerzas conservativas. Normalmente trabajaremos con las fuerzas conservativas más comúnes (peso, elástica, etc), así que pueden usar las fórmulas de sus potenciales como conocidas.

En nuestro Ejemplo tenemos dos contribuciones de la fuerza peso (una por cada partícula), así que la energía potencial total sería

\begin{equation*} U_g=-m_1gy_1-m_2gy_2\,, \end{equation*}

recuerden que definimos $\hat{y}$ hacia abajo.

Cuarto paso: Energía cinética

Debemos definir la energía cinética total del sistema a partir de la contribución de cada partícula, usando

\begin{equation*} K_i=\frac{1}{2}m|\vec{v}_i|^2\,, \end{equation*}

en el sistema de coordenadas que hayamos elegido.

Como en nuestro Ejemplo estamos utilizando coordenadas cartesianas, la energía cinética debido a dos partículas sería:

$$\begin{align*} K=\sum_i K_i=\frac{1}{2}m_1\left(\dot{x}_1^2 + \dot{y}_1^2\right)+\frac{1}{2}m_2\left(\dot{x}_2^2 + \dot{y}_2^2\right) \end{align*}$$

Quinto paso: Relaciones entre coordenadas

Este es un paso importante, debemos recordar la cantidad de grados de libertad del problema, que debería ser la misma cantidad de variables que tengamos en nuestro lagrangiano. Antes de utilizar Euler-Lagrange, debemos hacer matemáticamente explícita la relación/vínculo entre las coordenadas de las partículas del problema.

En el Ejemplo notamos que las coordenadas $x_i$ y $y_i$ se pueden escribir como

$$\begin{align*} x_1=l_1\sin\theta_1\,,&\quad y_1=l_1\cos\theta_1\\ x_2=l_1\sin\theta_1 + l_2\sin\theta_2\,,&\quad y_2=l_1\cos\theta_1 + l_2\cos\theta_2\\ \end{align*}$$

donde vemos explícitamente que $x_i$ y $y_i$ no son independientes, si no que están relacionadas entre sí por los ángulos $\theta_i$ (pueden ver que $x_1^2+y_1^2=l_1^2$, o sea están relacionadas directamente).

Derivando con respecto al tiempo estas coordenadas

$$\begin{align*} \dot{x}_1=l_1\cos\theta_1\dot{\theta}_1\,, &\quad \dot{y}_1=-l_1\sin\theta_1\dot{\theta}_1\\ \dot{x}_2=l_1\cos\theta_1\dot{\theta}_1 + l_2\cos\theta_2\dot{\theta}_2\,, &\quad \dot{y}_2=-l_1\sin\theta_1\dot{\theta}_1 -l_2\sin\theta_2\dot{\theta}_2\,,\\ \end{align*}$$

Usando estas expresiones, reemplazamos en las energías

$$\begin{align*} U&=-(m_1 + m_2)gl_1\cos\theta_1-m_2gl_2\cos\theta_2\\ K&=\frac{1}{2}m_1l_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2(l_1^2\dot{\theta}_1^2+l_2^2\dot{\theta}_2^2 + 2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2))\,,\\ \end{align*}$$

donde ahora si vemos explícitamente los dos únicos grados de libertad que necesitamos para describir el problema.

Sexto paso: Lagrangiano y ecuaciones E-L

A esta altura, lo complicado ya está hecho, solo basta reemplazar las energías en el lagrangiano, en nuestro Ejemplo sería

$$\begin{align*} L&=K-U\\ &=\frac{1}{2}m_1l_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2(l_1^2\dot{\theta}_1^2+l_2^2\dot{\theta}_2^2 + 2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2))\\ &\qquad +(m_1 + m_2)gl_1\cos\theta_1+m_2gl_2\cos\theta_2\,.\\ \end{align*}$$

Las coordeandas $q$ con las que debemos derivar en las ecuaciones de E-L

\begin{equation*} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)=\frac{\partial L}{\partial q}\,, \end{equation*}

son las variables con las que quedó definido el lagrangiano (después de haber hecho el vínculo entre las coordenadas en los pasos anteriores), en nuestro caso son: $\theta_1$ y $\theta_2$. Son solo derivadas, así que no vayan a equivocarse en este paso!!

Lae ecuación de movimiento para $\theta_1$ se calcularía como:

$$\begin{align*} \frac{\partial L}{\partial \theta_1}&=-(m_1+m_2)gl_1\sin\theta_1 -m_1l_1l_2\dot{\theta}_1\dot{\theta}_2\sin(\theta_1-\theta_2) \\ \frac{\partial L}{\partial \dot{\theta}_1}&=(m_1+m_2)l_1^2\theta_1+m_2l_1l_2\dot{\theta}_2\cos(\theta_1-\theta_2)\\ \end{align*}$$

así que la ec. E-L para $\theta_1$

\begin{equation*} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}_1}\right)-\frac{\partial L}{\partial \theta_1}=0 \end{equation*}

sería

$$\begin{align*} (m_1+&m_2)l_1^2\ddot{\theta}_2+m_2l_1l_2\left[\ddot{\theta}_2\cos(\theta_1-\theta_2)-\dot{\theta}_2(\dot{\theta}_1-\dot{\theta}_2)\sin(\theta_1-\theta_2)\right]\\ &+ m_1l_1l_2\dot{\theta}_1\dot{\theta}_2\sin(\theta_1-\theta_2)+(m_1+m_2)gl_1\sin\theta_1=0 \end{align*}$$

y para $\theta_2$, siguiendo los mismos pasos,

$$\begin{align*} m_2l_2^2\ddot{\theta}_2+&m_2l_1l_2\left[\ddot{\theta}_1\cos(\theta_1-\theta_2)-\dot{\theta}_1(\dot{\theta}_1-\dot{\theta}_2)\sin(\theta_1-\theta_2)\right]\\ -& m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\sin(\theta_1-\theta_2)+m_2gl_2\sin\theta_2 =0\,. \end{align*}$$

Estas ecuaciones de movimiento nos permiten modelar el movimiento que vemos en la imagen de abajo (calculado numéricamente).

Séptimo paso: Resolver el problema indicado

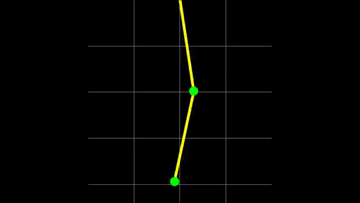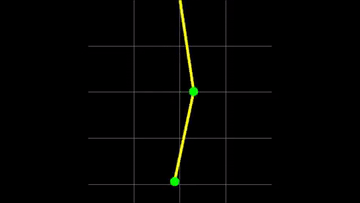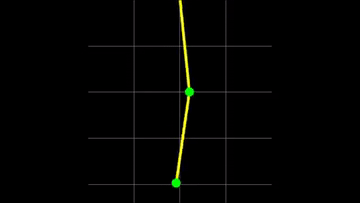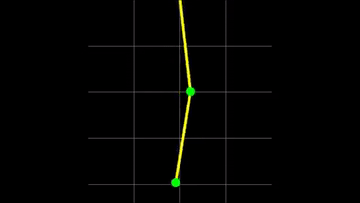
Como pueden ver en el .gif, el movimiento que sigue un péndulo doble es un movmiento caótico y, hasta lo que yo sé, no se ha podido calcular una solución analítica para las ecuaciones de movimiento (las encontradas) para cualquier ángulo $\theta_i$.

Es por esto que muchas veces uno se remite a considerar pequeños movimiento en torno a una posición de equilibrio estable. En particular, para el caso de más de 1 partícula podemos calcular los modos normales de oscilación, que es el tópico de la siguiente sección.

Subsección: Modos normales

Autovalores y autovectores

Hay ciertos problemas (no todos) que cuando tenemos más de 1 partícula, nos permite calcular puntos de equilibrio estables y considerar que todas las partículas oscilan en torno a estos puntos con la misma frecuencia de oscilación, pero pudiendo ir en el mismo sentido o sentidos contrarios.

Para calcular estas frecuencias de oscilación (imponemos común para todas las partículas), debemos linealizar las ecuaciones de movimiento y de esta forma poder escribirlas de forma matricial como sigue

Sistema EDOs/EOMs lineales

$$\begin{gather*} \ddot{\vec{r}}+\Omega^2\vec{r}=\vec{0}\\ \\ \Leftrightarrow\frac{d^2}{dt^2}\begin{pmatrix} q_1\\ q_1\\ \vdots\\ q_n \end{pmatrix} + \begin{bmatrix} \Omega^2_{11} & \Omega^2_{12} & \dotsb & \Omega^2_{1n}\\ \Omega^2_{21} & \Omega^2_{22} & \dotsb & \Omega^2_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ \Omega^2_{n1} & \Omega^2_{n2} & \dotsb & \Omega^2_{nn}\\ \end{bmatrix}\begin{pmatrix} q_1\\ q_1\\ \vdots\\ q_n \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ \vdots\\ 0 \end{pmatrix} \end{gather*}$$

que tiene la forma de un oscilador armónico simple.

Habiendo expresado la matriz $\Omega^2$ calculamos los autovalores $\omega^2$ con:

\begin{equation*} \textnormal{det}\left(\Omega^2_{n\times n} - \omega^2I_{n\times n}\right)=0\,, \end{equation*}

donde $\omega^2$ serían las frecuencias de los modos normales. Y los modos normales vendrían dados por los vectores propios asociados a cada valor propio (a cada $\omega^2_i$)

Modos normales

$$\begin{gather*} \left(\Omega^2_{n\times n}-\omega^2_iI_{n\times n}\right)\vec{v}_i=\vec{0}\\ \\ \Leftrightarrow\begin{pmatrix} \Omega^2_{11}-\omega^2_i & \Omega^2_{12} & \dotsb & \Omega^2_{1n}\\ \Omega^2_{21} & \Omega^2_{22}-\omega^2_i & \dotsb & \Omega^2_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ \Omega^2_{n1} & \Omega^2_{n2} & \dotsb & \Omega^2_{nn}-\omega^2_i\\ \end{pmatrix}\begin{pmatrix} v^1_i\\ v^2_i\\ \vdots\\ v^n_i\\ \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ \vdots\\ 0 \end{pmatrix} \end{gather*}$$

Recuerden que una vez calculados los autovectores $\vec{v}_i$ hay que normalizarlos.

Linealizar las ecs. de movmiento

Para utilizar el método de autovalores y autovectores necesitamos linealizar el sistema de EDOs que obtenemos. Esto lo podemos realizar en dos momentos del cálculo, según convenga:

Cuando conseguimos la expresión del lagrangiano (antes de usar E-L)
Cuando ya conseguimos las ecuaciones de movimiento

El segundo caso es cuando el cálculo no es tan complicado y podemos calcular las derivadas de E-L sin mayor problema. Sin embargo, si las derivadas llegasen a ser insufribles (y nos podrían conducir a equivocarnos derivando), tenemos que empezar aproximar el lagrangiano antes de calcular sus ecs. de movmiento. Enfoquémonos en este último caso.

Recordemos que para considerar pequeñas oscilaciones en torno a un punto de equilibrio estable $q_0$, hacíamos

\begin{equation}\label{eq:q-aprox} q(t)=q_0+\delta q(t)\quad \Rightarrow \quad \dot{q}(t)=\dot{\delta q}(t) \end{equation}

donde $|\delta q|\ll 1$, lo que nos permite hacer aproximaciones despreciando términos.

El principal objetivo es que cuando reemplazamos (\ref{eq:q-aprox}) en el lagrangiano que hayamos encontrado, debemos despreciar términos de forma de que al final quedemos con un lagrangiano a orden cuadrático en los $q_i$ y $\dot{q}_i$. En forma general algo como:

\begin{equation}\label{eq:lagrangiano-approx} \begin{aligned} L\approx& \sum_{i=1}^n(a_i\dot{\delta q^2_i} + b_i\delta q_i^2)\\ &+\sum_{i\neq j} (c_{ij}\dot{\delta q}_i\dot{\delta q}_j + d_{ij}\delta{q}_i\delta q_j) \end{aligned} \end{equation}

donde términos como $\delta x^2$ y $\delta x \delta y$ son del mismo orden (cuadrático) aunque no sean la misma variable.

Entonces, cuando derivamos en las ecs. de E-L con un lagrangiano como el de (\ref{eq:lagrangiano-approx}) quedamos solo términos lineales, por lo tanto las ecs. de movimiento también.

No hay una regla paso a paso para despreciar términos, ya que depende del problema y las funciones que nos queden dentro del lagrangiano (polinomios al cuadrado, raíces, funciones trigonométricas, etc), pero lo que siempre deben tener en cuenta es:

\begin{equation*} \delta q \gg \delta q^2 \gg \delta q^3 \gg \dotsb \gg \delta q^n \quad \textnormal{si} \quad |\delta q|\ll 1 \end{equation*}

entonces si en un mismo polinomio nos encontramos con perturbaciones con diferentes órdenes, nos quedamos con los términos de menor exponente y el resto los depreciamos. Todo siempre pesando en que debemos quedar con un lagrangiano de segundo orden.

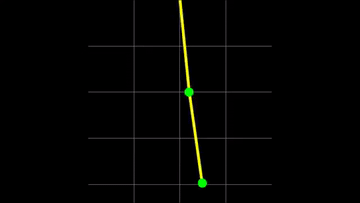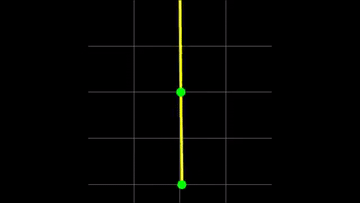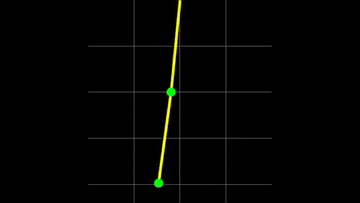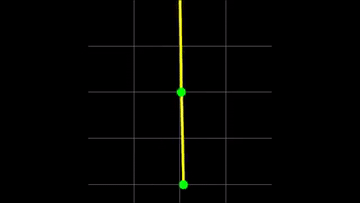
En el Ejemplo que estamos tratando, luego de hacer las aproximaciones en torno a los puntos de equilibrio estables $\theta_0=0$, conseguimos dos frecuencias de oscilación para dos modos normales de oscilación (ver auxiliar del Colipí), que pueden ver a continuación:

Mecánica FI2001