Notes | Dinámica

Este tópico se abarca en todo el resto del curso, por lo que es importante que lo entiendan bien.

La fórmula clave y con la que resolveremos los problemas es la segunda Ley de Newton:

\begin{equation}\label{eq:segundaley} m\vec{a}=\sum_i{\vec{F}}_i\,. \end{equation}

Para utilizar esta ecuación debemos realizar 7 pasos:

Primer paso: Hacerse una idea de cómo se mueve la partícula
Segundo paso: Identificar las fuerzas que están actuando sobre la partícula
Tercer paso: Escoger un sistema de coordendas adecuado para el movimiento de la partícula
Cuarto paso: Expresar matemáticamente las fuerzas en el sist. de coord. elegido
Quinto paso: Reemplazar las fuerzas y la aceleración en (\ref{eq:segundaley})
Sexto paso: Obtener la ecuación de movimiento vectorial, y con esto las ecuaciones de movimiento escalares
Séptimo paso: Calcular las cantidades que nos piden en el problema

Imaginar el movimiento

Antes de hacer cualquier cosa, hay que tomarse 5 minutos y utilizar la intuición física para imaginar, a grandes rasgos, cómo se movería la partícula que estamos tratando en el problema.

En algunos ejercicios tenemos fuerzas de restricción, como lo son la fuerza normal de las superficies y la tensión de las cuerdas. Estas fuerzas definen completamente cómo se mueven la partículas en ciertas direcciones, por lo que, sabiendo identificarlas, podemos hacernos una idea de dónde estará la partícula en un tiempo posterior.

Por ejemplo, en la siguiente Figura:

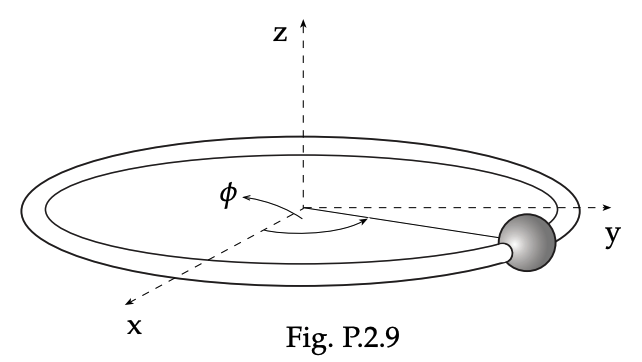
Description of the image — Fig.1 Problema de ejemplo

vemos que la fuerza normal del anillo produce que la partícula está restringida a moverse siguiendo una circunferencia (de radio $R$ por enunciado) y no tener movimiento en el eje $\hat{k}$.

Identificar las fuerzas

Como vemos en \eqref{eq:segundaley}, tenemos que identificar todas las fuerzas $\vec{F}_i$ que estén actuando directamente sobre la partícula de interés.

Algunas fuerzas nos las dan en el enunciado (normalmente fuerzas exóticas con una expresión particular), las otras hay que saber identificarlas, por ejemplo:

Si la partícula se mueve sobre una superficie $\Rightarrow$ fuerza normal
Si hay dos cuerpos con masa no despreciable $\Rightarrow$ fuerza gravitacional
Si hay cargas eléctricas $\Rightarrow$ fuerza de Coulomb
Si la partícula está atada a una cuerda $\Rightarrow$ tensión
Etc.

También, para elegir el sist. de coord. necesitamos saber en qué dirección apuntan estas fuerzas. A veces, apuntan siempre en una dirección en específico, y otras veces cambia en el tiempo y según dónde esté la partícula. Si sucede lo último, es un indicio que no debemos ocupar cartesianas.

Sistema de coordenadas

El sistema de coordenadas que vayamos a elegir para resolver nuestro problema puede definir sustancialmente la complejidad matemática. Aunque, teóricamente, cualquier problema de este curso puede ser resuelto usando cualquier sistema de coordenadas, una buena elección de este, basándonos en los pasos previos, nos puede ayudar mucho a reducir la cantidad de cálculos.

Debemos elegir un sist. tal que ambos lados de \eqref{eq:segundaley} queden lo más simple posible. Para simplificar el RHS (Right Hand Side), las fuerzas deben quedar descompuestas usando, ojalá, solo un vector unitario, o sea que las fuerzas apunten en un solo eje del sistema de coordenadas.

Mientras que para el LHS (Left Hand Side), buscamos que la mayor cantidad de términos posible se hagan 0.

Para el Ejemplo mostrado, tenemos que el movimiento es en una circunferencia, por lo que si escogemos coordenadas cilíndricas

\begin{equation*} \Rightarrow\dot{\rho}=\ddot{\rho}=0, \end{equation*}

ya que la distancia al origen no cambia en el tiempo. Y como no hay movimiento en $\hat{k}$

\begin{equation*} \Rightarrow\dot{z}=\ddot{z}=0, \end{equation*}

así que la aceleración de este problema, usando coordenadas cilíndricas, se simplifica mucho

$$\begin{align*} \vec{a}=&\,\big(\cancelto{0}{\ddot{\rho}} - \rho\dot{\phi}^2\big)\hat{\rho} + \big(2\cancelto{0}{\dot\rho}\dot\phi + \rho\ddot\phi\big)\hat{\phi} + \cancelto{0}{\ddot{z}}\hat{k}\\ =&\, -R\dot{\phi}^2\hat\rho + R\ddot\phi\hat\phi\,. \end{align*}$$

Expresar las fuerzas

Ya habiendo identificado las fuerzas, falta expresarlas matemáticamente en el sistema de coordenadas elegido.

Como mencioné en el Segundo Paso, hay fuerzas cuyas magnitudes y direcciones nos las dan por enunciado, así que en esos casos este paso ya está listo. Sin embargo, para problemas generales, debemos conocer con antelación las expresiones matemáticas de las fuerzas más comunes. Las 6 fuerzas que más se repiten en este curso las pueden ver en la sección: Fórmula de fuerzas.

Por ejemplo, para el problema que estamos tratando, para tener el movimiento circular necesitamos fuerzas en $\hat\rho$ y $\hat{k}$, que identificamos como fuerzas normales (independientes entre si), producidas por el aro y que permiten que la partícula no caiga verticalmente y que no salga disparada tangencialmente.

Así que, las fuerzas actuando sobre la partícula en el sist. de coord. escogido, quedarían descritas como:

\begin{equation*} \sum_i\vec{F}_i=N_\rho\,\hat{\rho} + N_z\,\hat{k} + mg\hat{k}. \end{equation*}

Notar que, aunque las fuerzas normales son comúnes en estos problemas, NO tienen una expresión general, ya que, como son fuerzas de restricción, sus expresiones matemáticas están dadas por las otras fuerzas del problema y el movimiento de la partícula. Entonces, cuando trabajamos con ellas, las dejamos como variables/incógnitas que calcularemos finalizando el problema.

Reemplazar

Lo más difícil ya está hecho, ahora solo debemos reemplazar lo encontrado en la aceleración $\vec{a}$ y en las fuerzas $\sum_i \vec{F}_i$. En el ejemplo mostrado, sería algo como:

$$\begin{align*} m\vec{a} &= \sum_i \vec{F}_i\\ \Leftrightarrow -R\dot{\phi}^2\hat\rho + R\ddot\phi\hat\phi&=N_\rho\,\hat{\rho} + N_z\,\hat{k} + mg\hat{k}\,, \end{align*}$$

con lo que conseguimos la ecuación de movimiento vectorial.

Ecuaciones de movimiento

En el paso anterior obtuvimos la ecuación de movimiento (o EoM por sus siglas en inglés), que resolviendo—integrando y ocupando las condiciones iniciales—obtendríamos toda la información del movimiento de la partícula. Sin embargo, uno prefiere trabajar con las ecuaciones de movimiento escalares

Para obtenerlas, notamos que, como trabajamos con una base de vectores unitarios ortonormales, al multiplicar la EoM vectorial por alguno de los vectores unitarios, obtenemos una ecuación (escalar) con únicamente los componentes que acompañan a ese vector unitario.

Para nuestro Ejemplo tendríamos las siguientes ecuaciones:

\begin{align*} \hat\rho)& \quad -R\dot{\phi}^2=N_\rho,\\ \hat\phi)& \quad R\ddot\phi=0,\\ \hat{k})& \quad 0=N_z + mg. \end{align*}

Para que lo tengan en mente, para movimientos en 3 dimensiones deberíamos obtener 3 ecuaciones de movimiento; para 2 dimensiones, 2 ecuaciones; y para 1 dimensión, 1 ecuación.

Calcular lo que nos piden

En este paso es donde los profes se ponen creativos. Las cosas más típicas que piden son:

¿Dónde se encuentra la partícula en un tiempo $t>0$?
Encuentre la velocidad angular de la partícula en función del ángulo
Calcule la expresión de la trayectoria $y=y(x)$
Calcule la tensión de la cuerda cuando la partícula describe un ángulo $\theta=\pi/2$ con respecto a la vertical
Etc.

Obviamente, estas son las preguntas que ustedes ven antes de comenzar a matraquear el problema. Sucede que en un principio se pueden ver muy complicadas, sin embargo, siempre van a tener que realizar este procedimiento que les enuncié.

Ya teniendo las EoMs escalares, es solo cuestión de matemática poder resolverlas. Aquí hay que ser creativos, ya que de haber fuerzas de restricción, las cuáles no conocemos, a priori, sus expresiones, no podemos simplemente integrar la ecuación correspondiente, ya que estas fuerzas son incógintas y no conocemos sus dependencias temporales ni espaciales.

Sin embargo, lo más típico es que una fuerza de restricción aparezca en más de una EoM escalar, por lo que podemos despejarla de una y reemplazarla en la otra. De esta forma buscamos obtener ecuaciones únicamente dinámicas (o sea, que solo aparezcan las coordenadas, sus derivadas, y constantes conocidas), donde podamos integrar sin problemas.

En el Ejemplo mostrado es un poco más sencillo, ya que, si nos pidieran calcular las expresiones de las fuerzas normales, $N_{\rho}$ y $N_z$ para algún $t>0$, notamos de inmediato que, en una primera instancia, no podemos hacer mucho con la ecuación de $\hat{\rho})$, ya que aparece $N_{\rho}$ que es una incógnita.

No obstante, la ecuación de $\hat{\phi})$ es puramente dinámica, así que podemos integrar con respecto al tiempo ambos lados de la ecuación,

\begin{align*} \int_0^t R \frac{\text{d}\dot{\phi}}{\text{d}t} \text{d}t &= 0\\ \Rightarrow R\int_{\dot{\phi}_0}^{\dot{\phi}(t)}\text{d}\dot{\phi} &= 0\\ \Rightarrow \dot{\phi}(t) &= \dot{\phi}_0 \end{align*}

donde ${\dot\phi}_0$ es la velocidad angular inicial (la dan por enunciado normalmente). Ahora sí, podemos reemplazar en $\hat{\rho})$ y obtener la expresión de la fuerza normal radial

\begin{equation*} N_\rho=-R{\dot{\phi}}_0^2. \end{equation*}

Mientras que para la normal vertical, de $\hat{k})$ es directo que $N_z=-mg$, por lo que finalmente la fuerza normal sería

\begin{equation*} \vec{N}=-R{\dot{\phi}}_0^2\hat{\rho} - mg\hat{k}. \end{equation*}

Fórmulas de fuerzas

Aunque hay problemas que utilizan fuerzas inventadas, hay un conjunto de fuerzas que son bien comunes en los problemas de este curso, recomiendo aprendérselas de memoria y saber cómo utilizarlas.

A continuación algunas de estas fuerzas:

Roce:
\begin{equation*} \vec{F}=-\mu N\,\hat{x} \end{equation*}
Roce viscoso:
\begin{equation*} \vec{F}(\vec{v})=-c\vec{v} \end{equation*}
Elástica:
\begin{equation*} \vec{F}(\vec{r})=-k(r-l_0)\,\hat{r} \end{equation*}
Gravitacional:
\begin{equation*} \vec{F}(\vec{r})=-G\frac{m_1m_2}{r^2}\hat{r} \end{equation*}
Gravitacional (cerca del suelo):
\begin{equation*} \vec{F}=-mg\,\hat{k} \end{equation*}
Coulomb:
\begin{equation*} \vec{F}(\vec{r})=k\frac{q_1q_2}{r^2}\hat{r} \end{equation*}

Material Complementario

¿De qué sirve esto?

En la siguiente animación pueden visualizar las órbitas de distintas estrellas que giran en torno al centro de nuestra Vía Láctea.

GIF — Animación hecha por: UCLA Galactic Center Group

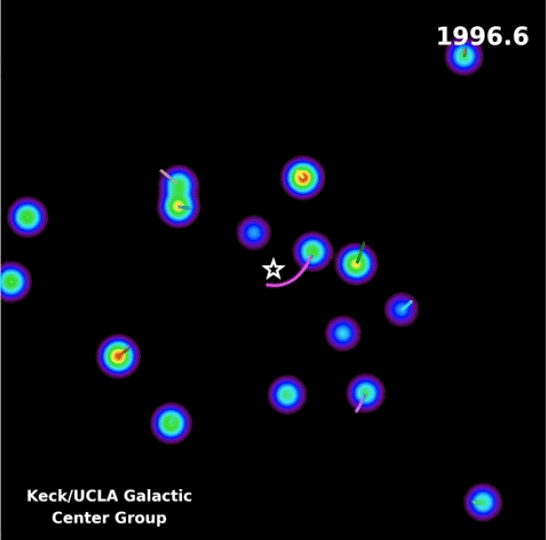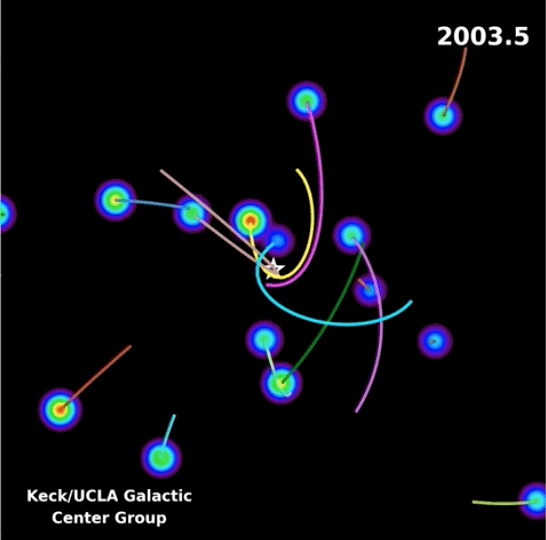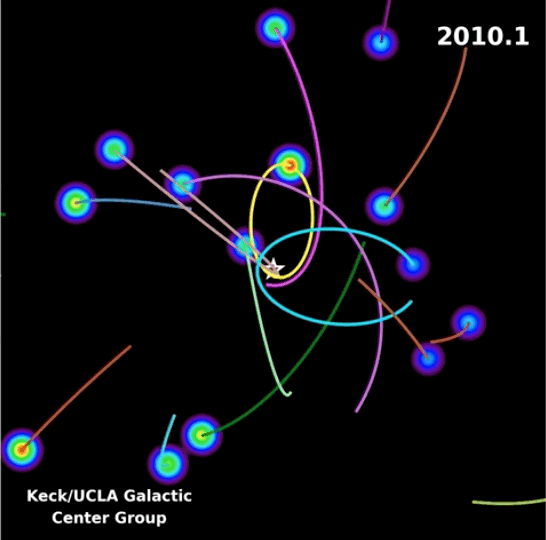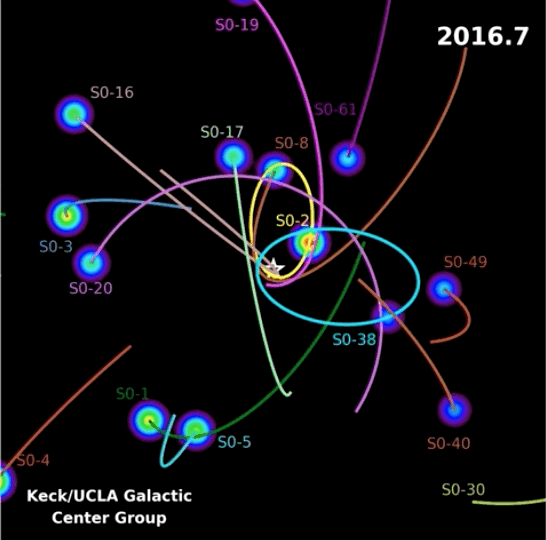
Esto es una clara evidencia de la presencia de un objeto muy masivo localizado en el centro de nuestra galaxia, en particular, de un agujero negro super masivo (SMBH) conocido como Sagitario A*.

De no existir este SMBH, y despreciando la atracción entre las mismas estrellas, la ecuación de movimiento de la $i$-ésima estrella sería

\begin{equation*} m_i\vec{a}_i = \vec{0}, \end{equation*}

lo que implica que seguirían trayectorias completamente rectas, lo que va en contra de las observaciones. Sin embargo, con la presencia de un SMBH de masa $M$ tendríamos algo como:

\begin{equation*} m_i\vec{a}_i = -G\frac{m_i M}{r_i^2}\hat{r}_i, \end{equation*}

que se puede resolver numéricamente para distintas condiciones iniciales y distintas masas $m_i$, y, utilizando las observaciones astronómicas, se puede estimar con mucha precisión la masa del agujero negro. En este caso, es algo como $M\approx 5\times 10^6\, M_{\odot}$, con $M_{\odot}$ la masa de nuestro Sol.

Auxiliares y evaluaciones

Si deseas profundizar más en esta unidad o ver cómo se resuelven problemas concretos, te invito a revisar los siguientes enlaces:

Mecánica FI2001