Prev. Section Next Section

Mecánica FI2001

Cinemática

GIF
Fig.1 Trayectoria, velocidad y aceleración de una partícula

Con cinemática nos referimos los problemas donde no nos interesa la forma/expresión de las fuerzas que están actuando, sino que ya nos dicen cómo estas afectan al movimiento del cuerpo. Realmente solo buscamos expresar el movimiento para tiempos y/o posiciones arbitrarias.

Recomiendo olvidar todas las fórmulas aprendidas en los cursos anteriores, en este curso aprenderemos a deducirlas todas.

La trayectoria de la partícula puede ser no trivial, así que en este curso introducimos 3 sistemas de coordenadas que usaremos según el caso.

Coordenadas cartesianas
$$\begin{gather*} \vec{r}=x\hat{i} + y\hat{j} + z\hat{k}\\ \dot{\vec{r}} = \dot{x}\hat{i} + \dot{y}\hat{j} + \dot{z}\hat{k}\\ \ddot{\vec{r}} = \ddot{x}\hat{i} + \ddot{y}\hat{j} + \ddot{z}\hat{k}\\ \end{gather*}$$
Coordenadas cilíndricas
$$\begin{align*} \vec{r} =& \,\rho\hat{\rho} + z\hat{k}\\ \dot{\vec{r}} =& \,\dot{\rho}\hat{\rho} + \rho\dot{\phi}\hat{\phi} + \dot{z}\hat{k}\\ \ddot{\vec{r}} =& \,\left(\ddot{\rho} - \rho\dot{\phi}^2\right)\hat{\rho} + \left(2\dot\rho\dot\phi + \rho\ddot\phi\right)\hat{\phi} + \ddot{z}\hat{k}\\ =& \,\left(\ddot{\rho} - \rho\dot{\phi}^2\right)\hat{\rho} + \frac{1}{\rho}\frac{d}{dt}\left(\rho^2\dot\phi\right)\hat\phi + \ddot{z}\hat{k}\\ \end{align*}$$
Coordenadas esféricas
$$\begin{align*} \vec{r} =& \,r\hat{r}\\ \dot{\vec{r}} =& \,\dot{r}\hat{r} + r\dot\theta\hat\theta + r\dot\phi\sin\theta\hat\phi\\ \ddot{\vec{r}} =& \,\left(\ddot{r} - r\dot\theta^2 - r\dot\phi^2\sin^2\theta\right)\hat{r} + \left(r\ddot{\theta} + 2\dot{r}\dot\theta - r\dot\phi^2\sin\theta\cos\theta\right)\hat\theta + \left(r\ddot\phi\sin\theta + 2\dot{r}\dot\phi\sin\theta + 2r\dot\phi\dot\theta\cos\theta\right)\hat{\phi}\\ =& \,\left(\ddot{r} - r\dot\theta^2 - r\dot\phi^2\sin^2\theta\right)\hat{r} + \left(r\ddot{\theta} + 2\dot{r}\dot\theta - r\dot\phi^2\sin\theta\cos\theta\right)\hat\theta +\frac{1}{r\sin\theta}\frac{d}{dt}\left(r^2\dot\phi\sin^2\theta\right)\hat{\phi}\\ \end{align*}$$

¿Qué se calcula en cinemática?

En cada problema nos dan información distinta y, por lo tanto, nos piden cosas también distintas. Lo más típico es que pidan calcular los tiempos cuando suceden ciertos eventos, por lo que necesitamos tener la posición o la velocidad en función del tiempo.

Por ejemplo, si queremos calcular la posición $r(t)$ y para esto nos dan la aceleración en todo tiempo, debemos integrar dos veces. Esquemáticamente sería algo como:

\begin{equation*} \vec{a}(t)\xrightarrow{\int \textnormal{d}t}\vec{v}(t)\xrightarrow{\int \textnormal{d}t}\vec{r}(t)\,. \end{equation*}

Y si nos dan la posición y necesitamos la velocidad (por ejemplo si queremos saber cuándo la partícula se detiene), debemos derivar 1 vez:

\begin{equation*} \vec{r}(t)\xrightarrow{d/dt}\vec{v}(t)\xrightarrow{d/dt}\vec{a}(t)\,. \end{equation*}

Ejemplos

A veces nos dan las expresiones de las coordenadas en cierto sistema. Por ejemplo:

"Ejercicio 1, 2023: Considere una curva espiral descrita en coordenadas esféricas por las ecuaciones:
\begin{equation*} r=R\,,\qquad\dot{\theta}=\omega_0\,,\qquad \phi=N\theta \end{equation*}
exprese la velocidad $\vec{v}$ y la aceleración $\vec{a}$ en esféricas."

por lo que debemos integrar (ya que nos dan $\dot{\theta}$ y no $\theta\,$) y derivar estas expresiones para reemplazar en las fórmulas mencionadas más arriba.

Muchos problemas en cinemática son problemas geométricos, por lo que usamos relaciones como el teorema del coseno

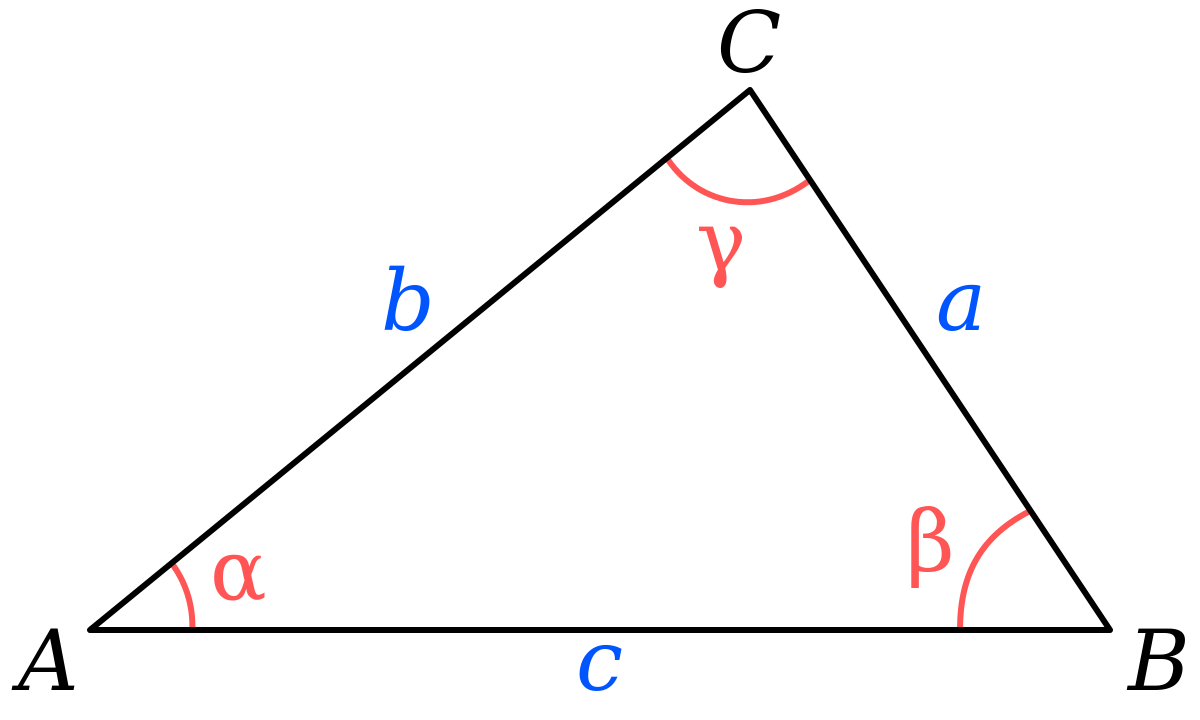
Description of the image
Fig.2 Triángulo arbitrario que sigue $c^2=a^2+b^2-2ab\cos\gamma$

que puede ser usado en un problema como el siguiente:

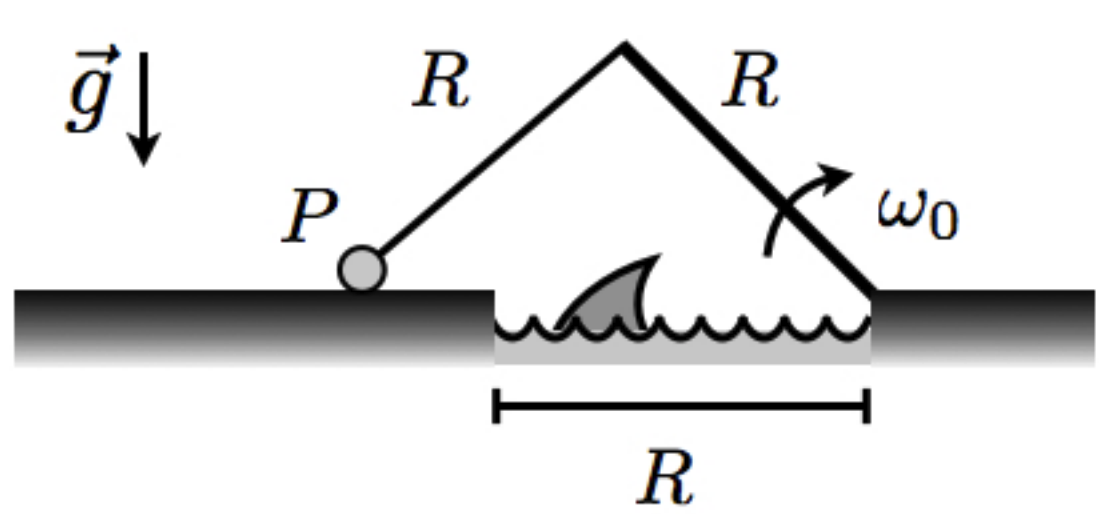
Description of the image
Fig.3 Problema 3 Control 1 del 2013, donde la vara de la derecha rota con velocidad angular $\omega_0$ constante

Errores comunes

Un error muy común es que al integrar la aceleración y la velocidad, saquen términos de la integral como si fueran constantes. Para hacer esto tienen que conocer la dependencia de cada término, no necesariamente su expresión explícita (que puede ser el objetivo del problema), sino que, por ejemplo, pensar:

¿a lo largo del movimiento cambia la distancia al origen?

En el caso que cambiara $\Rightarrow\rho$ depende del tiempo y hay que considerarlo al integrar y al derivar.

Esto pasa mucho con los vectores unitarios. Recordar que para coord. cilíndricas y esféricas los vectores unitarios dependen del tiempo, por lo que normalmente no se pueden sacar de una integral.

\begin{equation*} \frac{\textnormal{d}\hat{\rho}}{\textnormal{d}t}=\dot\phi\hat\phi\,,\qquad \frac{\textnormal{d}\hat\phi}{\textnormal{d}t}=-\dot\phi\hat{\rho} \end{equation*}

También hay que tener cuidado con no estar integrando o derivando cantidades evaluadas en un tiempo específico (que sería una constante), revisen lo que están haciendo cuando les pase esto.