Mecánica FI2001

Sesión 3

Parte 1: Lagrangiano y modos normales

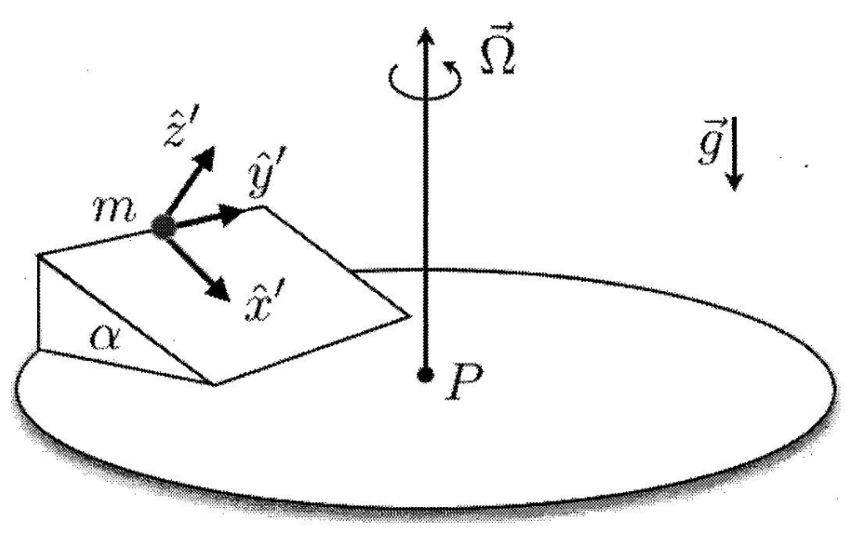
Considere un péndulo de largo $l$ y masa $m$ que pende de otro péndulo idéntico, de igual largo e igual masa (ver figura). La masa del péndulo superior tiene una carga positiva $q$. Aparte del campo gravitacional, en este sistema existe un campo eléctrico $\vec{E}=E_0\hat{j}$ donde $E_0$ es una constante positiva. Dicho campo ejerce una fuerza $\vec{F}_q=q\vec{E}$ sobre la carga

Derive el sistema de ecuaciones de movimiento para pequeñas oscilaciones en torno a $\phi_1=\phi_2=0$
Para el caso $qE_0=mg$, determine las frecuencias y modos normales del sistema. Bosqueje los modos normales (Puede usar $\sqrt{5}\approx 2.2$)

Hints P1

Utilice coordenadas cartesianas para describir la posición, $(x_1,\,y_1)$ y $(x_2,\,y_2)$, y velocidad de las partículas, $(\dot{x}_1,\,\dot{y}_1)$ y $(\dot{x}_2,\,\dot{y}_2)$.
La energía potencial gravitatoria de cada partícula sería

\begin{equation*} U_{gi}=mgy_i \end{equation*}
Ocupando

\begin{gather*} \vec{F}=-\nabla U \end{gather*}

como la fuerza eléctrica $\vec{F}=qE_0\hat{j}$ solo es en $\hat{j}$ ocupamos el gradiente en cartesianas

\begin{gather*} qE_0\hat{j}=-\frac{\partial U_{E}}{\partial y}\hat{j}\\ \Rightarrow U_{E}=-qE_0y_1 \end{gather*}

Solo tendríamos 1 potencial asociado a la fuerza eléctrica, ya que solo la partícula 1 tiene carga eléctrica.
El lagrangiano no puede quedar expresado en función de $(x_i,\,y_i)$. Busque expresar estas coordenadas cartesianas (de ambas partículas) usando los ángulos $\phi_1$, $\phi_2$ y la longitud $l$, para conseguir las siguientes relaciones:

\begin{gather*} x_1=l\sin\phi_1\,,\\ y_1=-l\cos\phi_1\,\\ x_2=l\sin\phi_1 + l\sin\phi_2\,,\\ y_2=-l\cos\phi_1 - l\cos\phi_2\,, \end{gather*}

(ojo con el signo de $y_i$). Estas relaciones tienen que derivarlas en función del tiempo para encontrar $\dot{x}_i$ e $\dot{y}_i$ y así expresar la energía cinética

\begin{equation*} K=\frac{1}{2}m(\dot{x}_1^2 + \dot{y}_1^2) + \frac{1}{2}m(\dot{x}_2^2 + \dot{y}_2^2) \end{equation*}

en función de $\phi_i$ y $\dot{\phi}_i$
Calculen las ecuaciones de movimiento antes de linealizar.

Ya con las ecs. de movimiento, como el punto de equilibrio es en $\phi_i^0=0$, las perturbaciones serían como

\begin{equation*} \phi_1(t)=\delta\phi_1(t)\,,\quad \phi_2(t)=\delta\phi_2(t) \end{equation*}

siempre con $|\delta\phi_i|\ll 1 $
Ya con las ecs. de movimiento linealizadas, identifiquen la matriz $\Omega_{2\times 2}^2$. Para calcular las frecuencias y los modos normales tienen que ocupar

\begin{equation*} \textnormal{det}(\Omega_{2\times 2}^2-\omega^2\cdot I)=0 \end{equation*}

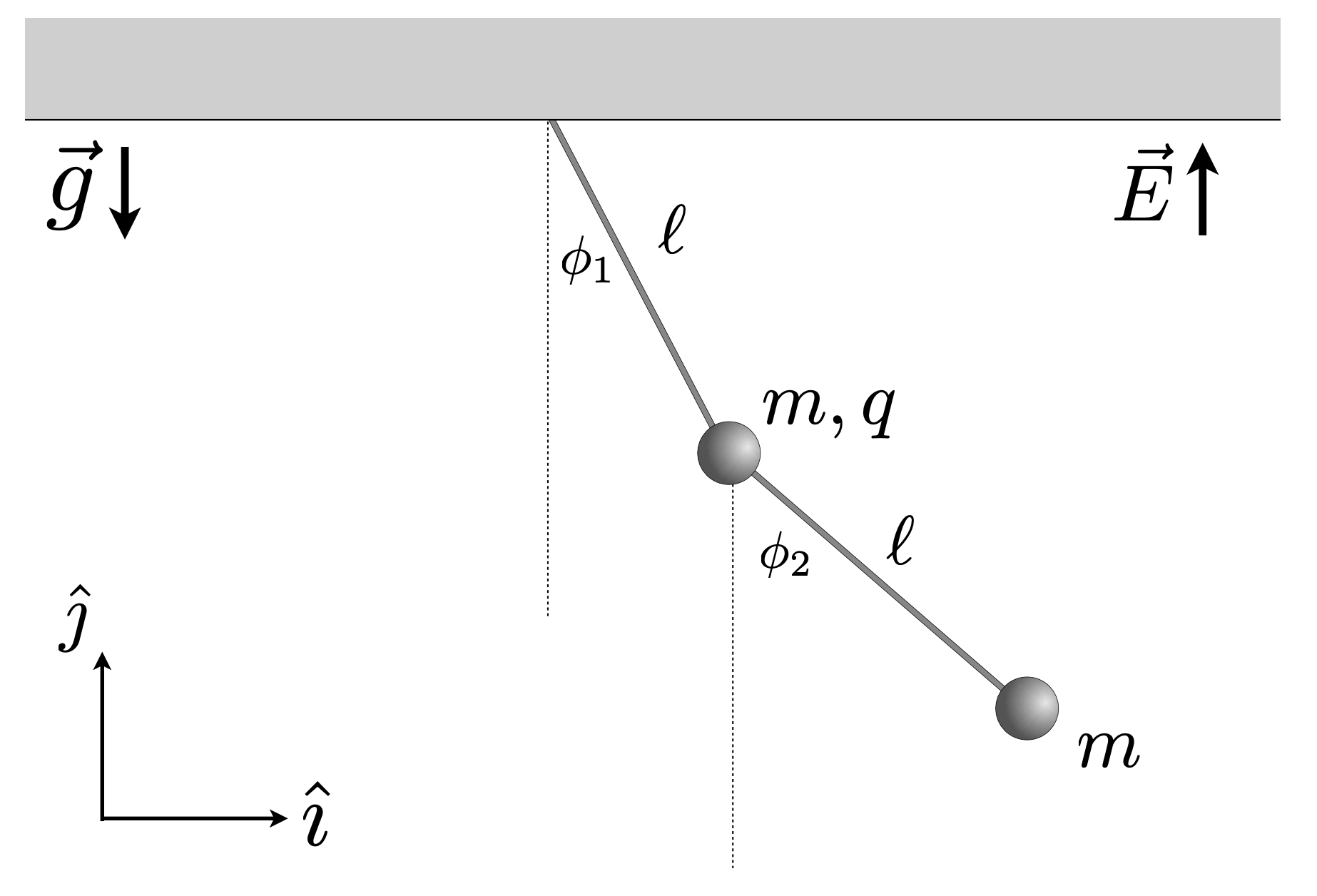
El bloque (1) de la figura tiene masa $m$, permanece conectado a la pared $\mathcal{O}$ mediante un resorte $(k,D)$ y puede deslizar sin roce sobre una superficie horizontal de largo $L$. El bloque (1) sostiene a un segundo bloque (2) de masa $m$ que cuelga verticalmente mediante una cuerda ideal inextensible de largo $L$ que pasa por la polea $P$. El segundo bloque sostiene a un tercer bloque (3) de masa $2m$ mediante un resorte $(k,D)$. Use la coordenada $y$ para designar la distancia de (1) desde $\mathcal{O}$ y la coordenada $x$ para designar la distancia de 3 desde $P$ (ver figura).

Obtenga el Lagrangiano del problema y con este las ecuaciones de movimiento de las 3 masas
Obtenga expresiones para las posiciones de equilibrio estable $x_{eq}$ y $y_{eq}$ en términos de los datos del problema
Escriba las ecuaciones de movmiento para pequeñas oscilaciones, considerando $x=x_{eq}+\delta x$ e $y=y_{eq} + \delta y$
Ideintifique la matriz de frecuencias $\Omega^2$ y determine las frecuencias de oscilación de los modos normales
Deduzca los modos normales de oscilación correspondiente a cada frecuencia obtenida en la parte anterior

Hints P2

Solo tenemos dos grados de libertad (serían 3, pero dos partículas están atadas por una cuerda inextensible), así que relacionando las coordenadas tendríamos:

\begin{gather*} (x_1,y_1)=(0,\, y_1)\,,\\ (x_2,y_2)=(y_1,L)\,,\\ (x_3,y_3)=(x_3,L)\,, \end{gather*}

donde por geometría y valores del problema encontramos que $x_2=y_1$, así que en todos los cálculos que aparezca $x_2$ lo cambiaremos por $y_1$ (por ejemplo en la energía potencial).
Si definimos el potencial gravitatorio como 0 en $x=0$, solo (2) y (3) tendrían potencial gravitatoria

\begin{gather*} U_{g2}=-mgx_2=-mgy_1\,,\\ U_{g3}=-mgx_3 \end{gather*}
Como tenemos dos resortes, habrían dos contribuciones a la potencial elástica

\begin{gather*} U_{e1}=\frac{1}{2}k(y_1 - D)^2\,,\\ U_{e2}=\frac{1}{2}k((x_3-x_2) - D)^2=\frac{1}{2}k((x_3-y_1) - D)^2 \end{gather*}
Deberían obtener dos ecuaciones de movimiento (tienen dos grados de libertad), entonces para calcular los puntos de equilibrio deben imponer $\ddot{y}_1=\ddot{x}_3=0$, con lo que conseguirían un sistema algebraico en el que pueden despejar $x_{3eq}$ y $y_{1eq}$
Ya con las ecs. de movimiento linealizadas, identifiquen la matriz $\Omega_{2\times 2}^2$ y para calcular las frecuencias y los modos normales tienen que ocupar

\begin{equation*} \textnormal{det}(\Omega_{2\times 2}^2-\omega^2\cdot I)=0 \end{equation*}

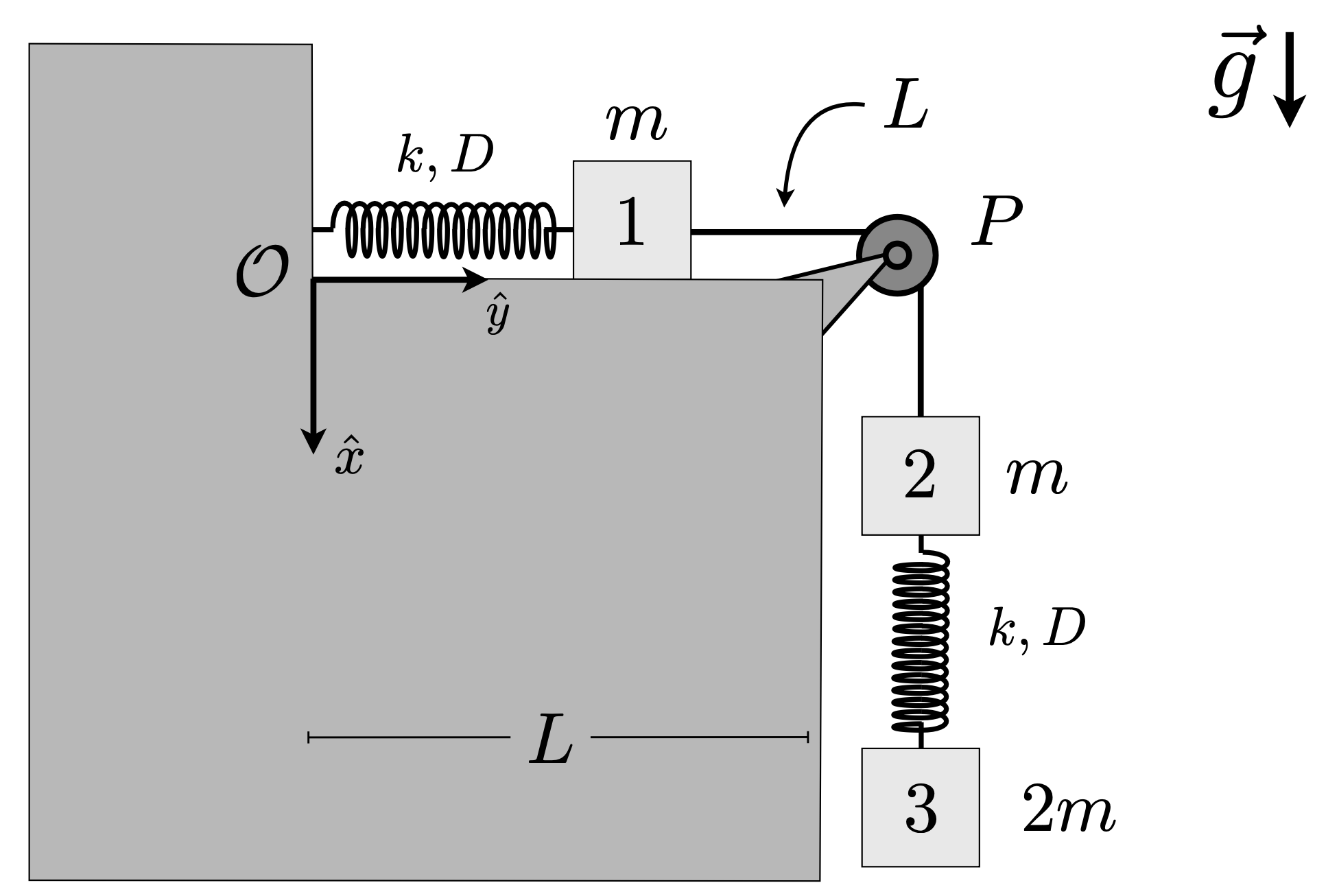
Un cono hueco de radio $R$ y altura $R$, tiene un orificio pequeño en su extremo superior por el cual pasa una cuerda inextensible de largo $R$. Los extremos de la cuerda sostienen dos masas idénticas $m$, una de las cuales permanece unida a la base del cono mediante un resorte $k$ de largo natural $D = \frac{mg}{k}\left(1-\frac{1}{\sqrt{2}}\right)$, mientras que la otra desliza sin roce sobre la superficie del cono. Utilice la coordenada $r$ para denotar la distancia de la segunda masa a la punta del cono, y $\phi$ para denotar el ángulo entre la proyección de la cuerda sobre la base y un eje fijo (ver figura). En $t=0$ se tienen $r=r_0$, $\dot{r}=0$, $\phi=0$, $\dot{\phi}=\omega_0$.

Determine el Lagrangiano del sistema para las variables $r$ y $\phi$
Obtenga las ecuaciones de Euler-Lagrange
Integre la ecuación para el ángulo $\phi$ y utilice su resultado para obtener una ecuación de movimiento exclusivamente en términos de $r$
Determine el valor que debe tener la velocidad angular $\omega_0$ para que $r$ se mantenga constante ($r=r_0$)
Para el valor $\omega_0$ encontrado en la parte anterior, obtenga la ecuación de pequeñas oscilaciones para $\delta r\equiv r-r_0$. Determine la frecuencia de pequeñas oscilaciones

Hints P3

Para describir las energías potenciales (dos gravitacionales y una elástica), solo necesitamos conocer la altura de las partículas, que describiremos en función de $r$.

Para la partícula dentro del cono tenemos

\begin{equation*} z_1=R-(R-r)=r \end{equation*}

y para la partícula sobre el manto

\begin{equation*} z_2=R-r\cos\pi/4 \end{equation*}

donde el $\pi/4$ sale de la forma del cono (radio y altura $R$ $\Rightarrow$ triángulo rectángulo)
Las energía potenciales gravitatorias estarían dadas por

\begin{gather*} U_{g1}=mgz_1\,,\\ U_{g2}=mgz_2 \end{gather*}

donde definimos esta energía como 0 a la altura de la base del cono y las altura son positivas hacia arriba.
La energía potencial elástica (solo una porque solo hay un resorte) estaría dada por

\begin{equation*} U_e=\frac{1}{2}k(z_1-D)^2 \end{equation*}
Usando coordenadas esféricas (con origen en la punta del cono, así que $\theta=3\pi/4$) para la partícula del manto y coordenadas cartesianas para la partícula dentro del cono, la energía cinética sería

\begin{equation*} K=\frac{1}{2}m(\dot{r}^2 + r^2\dot{\phi}^2\sin^2(3\pi/4))+\frac{1}{2}m\dot{z}_1^2 \end{equation*}
Debemos integrar la ecuación de movimiento de $\phi$ (la que tiene $\ddot{\phi}$) para obtener una expresión de $\dot\phi$ en función de $r$ y así reemplazar este $\dot\phi=\dot\phi(r)$ en la ec. de movimiento de $r$ (la que tiene $\ddot{r}$) y que esta quede en función únicamente de $r$ y $\ddot{r}$.

Esto se debe a la conservación del momentum angular, ya que no hay fuerzas en la dirección de $\hat\phi$.
Para 4., que $r$ sea constante quiere decir que $r=r_0$ sea un punto de equilibrio estable, o sea debemos imponer $\ddot{r}=0$ y despejar el $\dot\phi=\omega_0$ que cumpla esto (tendríamos que ocupar la ec. de mov. de $r$ antes de hacer el ítem 3.)
Linealizamos la ecuación de movimiento en $r$ ($\ddot{r}=\ddot{r}(r)$), con lo que obtendríamos la ec. de un oscilador armónico

\begin{equation*} \ddot{\delta r} + \omega^2\delta r + c=0\,, \end{equation*}

donde $c$ sería una constante positiva conocida y $\omega^2$ sería la frecuencia de pequeñas oscilaciones de nuestro problema.

Parte 2: Sistemas de referencia no inerciales

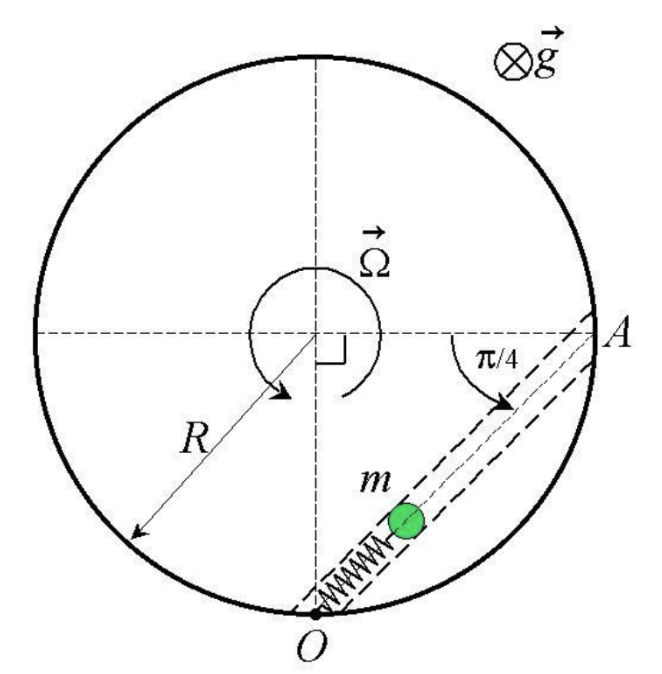
Una partícula $P$ de masa $m$ puede deslizar sin roce por el interior de un tubo $OA$, que a su vez está fijo a un aro de radio $R$, con la geometría que se indica en la figura. La partícula está unida al extremo de un resorte de constante elástica $k$ y largo natural cero, cuyo otro extremo está fijo al punto $O$

El argo gira en torno a un eje vertical que pasa por su centro, con velocidad angular constante $\vec{\Omega}$, donde $\Omega=k/2m$

Si inicialmente $P$ se encuentra en el punto medio entre $O$ y $A$, y su velocidad relativa al tubo es $v_0$ en la dirección de $O$ hacia $A$. Determine

La posición de $P$ relativa al tubo en función del tiempo
La reacción que ejerce el tubo a $P$

Hints P4

Defina el sistema de coordenadas de $S'$ como un sistema (solidario con el movimiento) cartesiano con origen en $O$, $\hat{x}'$ apuntando en la dirección del tubo y $\hat{k}'$ saliendo de la pantalla. De esta forma

\begin{equation*} \begin{aligned} \vec{r}^{\,\prime}&=x'\hat{x}'\\ \Rightarrow {\dot{\vec{r}}}^{\,\prime}&=\dot{x}'\hat{x}'\\ \Rightarrow {\ddot{\vec{r}}}^{\,\prime}&=\ddot{x}'\hat{x}' \end{aligned} \end{equation*}
Defina el sistema de coordenadas de $S$ como un sistema cilíndrico con origen en el centro de la circunferencia y $\hat{\rho}$ apuntando al punto $O$ (el origen de $S'$). De esta forma

\begin{equation*} \begin{aligned} \vec{R}&=R\hat{\rho}\\ \Rightarrow \dot{\vec{R}}&=\dotsb \\ \Rightarrow \ddot{\vec{R}}&=\dotsb \end{aligned} \end{equation*}

calculen ustedes estas derivadas usando $d\hat{\rho}/dt=\dot{\phi}\hat{\phi}$ y $d\hat{\phi}/dt=-\dot{\phi}\hat{\rho}$.
La velocidad angular $\vec{\Omega}$ estaría dada por $\vec{\Omega}=\Omega\hat{k}$, con $\hat{k}$ del sistema cilíndrico de $S$.
Las fuezas reales son: fuerza elástica, fuerza peso y dos fuerzas normales ejercidas por el tubo

\begin{gather*} \vec{F}_e=-kx'\hat{x}'\,,\\ \vec{F}_P=-mg\hat{k}'\,,\\ \vec{N}=N_{y'}\hat{y}'+ N_{k'}\hat{k}' \end{gather*}
Escriba los ejes del sistema de $S$ (el cilíndrico) en los ejes del sistema $S'$ (el cartesiano) para poder escribir $\ddot{\vec{R}}$ y $\vec{\Omega}$ en los ejes $(\hat{x}',\hat{y}',\hat{z}')$
Reemplace todo lo encontrado en:

\begin{equation*} m\ddot{\vec{r}}^{\,\prime} = \vec{F} - m\ddot{\vec{R}} - m\vec{\Omega}\times(\vec{\Omega}\times \vec{r}^{\,\prime}) - 2m\vec{\Omega}\times \dot{\vec{r}}^{\,\prime} - m\dot{\vec{\Omega}}\times\vec{r}^{\,\prime} \end{equation*}

Luego separe esta ecuación de movimiento vectorial en las 3 ecuaciones de movimiento escalar (una para $x'$, otra para $y'$ y otra para $z'$, estas últimas dos estarían igualadas a 0 ya que $\ddot{y}'=\ddot{z}'=0$). Resuelva la ecuación de mov. de $x'$ y así conseguirá $x'(t)$, que es lo que piden en 1.
Para 2., ya con $x'(t)$ reemplace en las ecs. de mov. escalares de $\hat{y}'$ y $\hat{z}'$ para conseguir $N_{y'}$ y $N_{k'}$

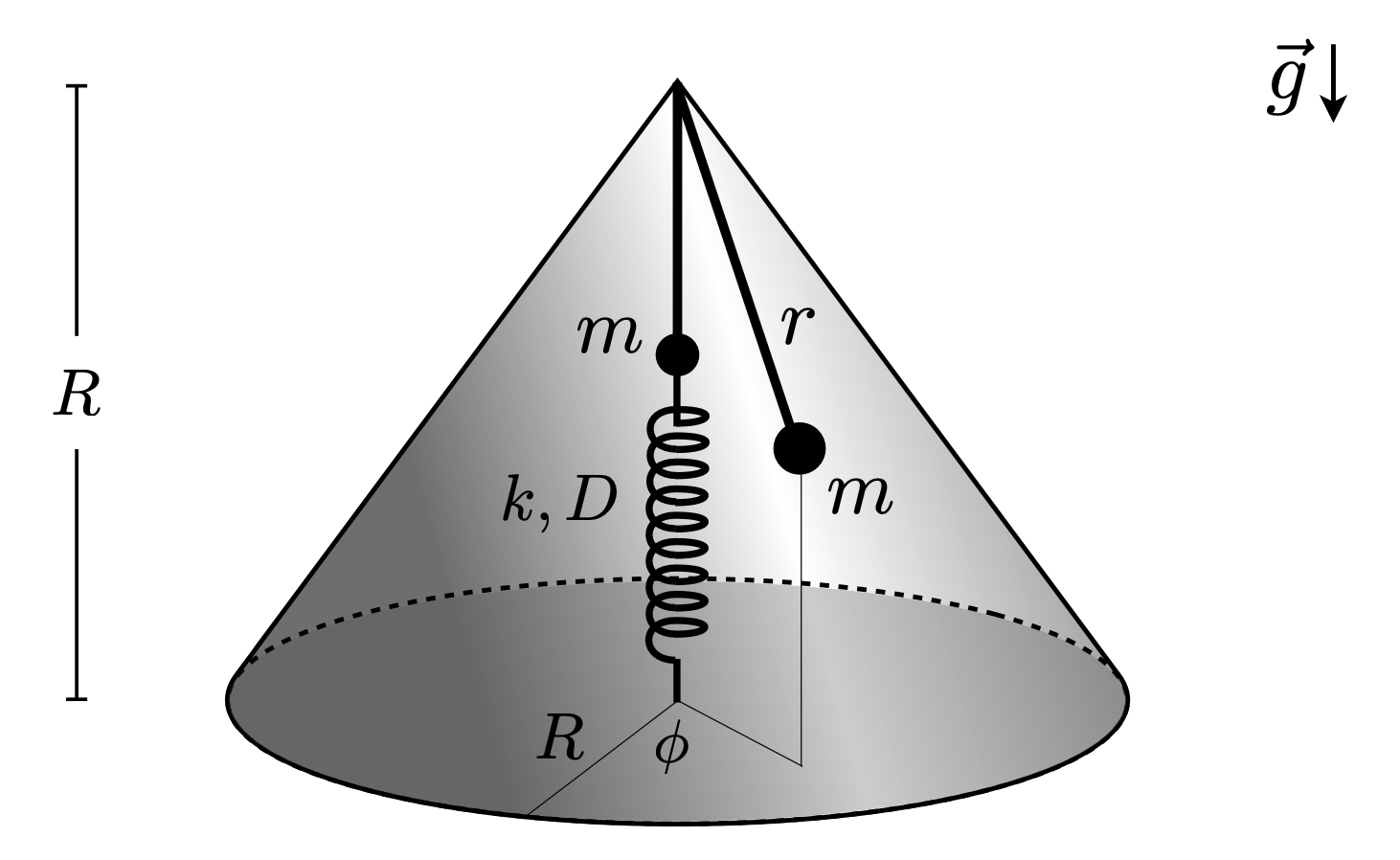
Una cuña de ángulo $\alpha$ respecto de la horizontal se ubica sobre una plataforma que rota con velocidad angular constante $\Omega$ respecto de un eje vertical que pasa por un punto $P$, como muestra la figura. Una partícula de masa $m$ es liberada sobre la cuña partiendo su movimiento desde el resposo relativo a la cuña y su movimiento es descrito con respecto al sistema móvil $S'=\{\hat{x}',\hat{y}',\hat{z}'\}$ indicado en la figura, cuyo origen se ubica en la posición inicial de la partícula sobre la cuña. Considere en este problema que pueden despreciarse todas las fuerza inerciales excepto la fuerza de Coriolis. Se pide:

Escribir la ecuación de movimiento de la partícula en sus 3-componentes $x',\, y',\, z'$ del sistema de referencia móvil
Resolver las ecuaciones, encontrando $x'(t)$ e $y'(t)$. Ver indicación de más abajo
Esquematizar la trayectoria de la partícula sobre la cuña. Determinar el máximo descenso y la máxima rapidez (relativa) de la partícula en su movimiento

Indicación: La ecuación diferencial $\dddot{u}=A-\omega_0^2\dot{u}$, con $A$ y $\omega_0$ constantes, tiene por solución general:

\begin{equation*} u(t)=\frac{A}{\omega_0^2}t + C_1\cos(\omega_0t) + C_2\sin(\omega_0 t)+C_3 \end{equation*}

donde las constantes $C_1,\,C_2,\, C_3$ se determinan según las condiciones inciales $u(0),\, \dot{u}(0),\, \ddot{u}(0)$.

Hints P5

Como recomienda el enunciado, defina el sistema de coordenadas de $S'$ como un sistema de coordenadas cartesiano solidario con el movimiento de la cuña y con $\hat{k}'$ perpendicular a la cuña. No importa a qué distancia se encuentra del punto $P$, ya que despreciamos la fuerza ficticia asociada a $-m\ddot{\vec{R}}$.

De esta forma la posición de la partícula (en el sistema $S'$) está dada por:

\begin{equation*} \begin{aligned} \vec{r}^{\,\prime}&=x'\hat{x}' + y'\hat{y}'\\ \Rightarrow {\dot{\vec{r}}}^{\,\prime}&=\dot{x}'\hat{x}' + \dot{y}'\hat{y}'\\ \Rightarrow {\ddot{\vec{r}}}^{\,\prime}&=\ddot{x}'\hat{x}' + \ddot{y}'\hat{y}' \end{aligned} \end{equation*}
Defina el sistema de coordenadas de $S$ como un sistema cilíndrico centrado en $P$, con $\hat{k}$ apuntando verticalmente y perpendicular al disco y con $\hat\rho$ apuntando al sistema $S'$
La velocidad angular estaría dada por $\vec{\Omega}=\Omega \hat{k}$
Las fuerzas reales actuando sobre la partícula serían: fuerza peso y fuerza normal

\begin{gather*} \vec{F}_P=-mg\hat{k}\,,\\ \vec{N}=N\hat{z}' \end{gather*}
Busque expresar $\hat{k}$ de $S$ en función de $\hat{x}'$ y $\hat{z}'$ de $S'$ (usando el ángulo $\alpha$) para poder expresar $\vec{F}_P$ con los ejes de $S'$. Habiendo hecho este y los pasos anteriores, reemplace en

\begin{equation*} m\ddot{\vec{r}}^{\,\prime} = \vec{F} - 2m\vec{\Omega}\times \dot{\vec{r}}^{\,\prime} \end{equation*}

Recordar que de las fuerzas ficticias, solo nos quedamos con Coriolis por enunciado.
Con el paso anterior conseguirá la ec. de movimiento vectorial, separe esta ecuación en las 3 ecuaciones de movimiento escalares.

Notará que las ecs. de $\hat{x}'$ e $\hat{y}'$ están acopladas, por lo que derívelas una vez y reemplace con las ecs. escalares originales para desacoplarlas.
Ya con las ecs. desacopladas, deberían tener algo como ${\dddot{x}}^{\,\prime }={\dddot{x}}^{\,\prime }(\dot{x}')$ e ${\dddot{y}}^{\,\prime }={\dddot{y}}^{\,\prime }(\dot{y}')$, así que utilice la Indiación para encontrar $x'(t)$ e $y'(t)$.

Las condiciones iniciales serían:

\begin{equation*} x'(0)=y'(0)=0\,,\quad \dot{x}'(0)=\dot{y}'(0)=0 \end{equation*}

y para $\ddot{x}'(0)$ e $\ddot{y}'(0)$ evalue en $t=0$ las ecs. de movimiento escalares originales.