Mecánica FI2001

Sesión 1

Parte 1: Cinemática

Un tubo gira sobre el plano $xy$ en torno al punto $\mathcal{O}$ con una velocidad angular $\vec{\omega}=\omega_0\hat{z}$, En el interior del tubo se desplaza una partícula, tal que su distancia al origen a lo largo del tubo viene dada por $D(t)=R\cos{(\omega_0 t)}$ (tomando valores positivos y negativos). En $t=0$ el eje del tubo coincide con el eje $\hat{x}$

Encuentre el vector posición $\vec{r}$ de la partícula (exprese su resultado en términos de los ejes $\hat{x}$ y $\hat{y}$)
Encuentre expresiones para la velocidad $\vec{v}$, rapidez $\nu=||\vec{v}||$ y aceleración $\hat{a}$ para todo tiempo (exprese sus resultados en términos de los ejes $\hat{x}$ y $\hat{y}$)
Encuentre los vectores tangencial $\hat{t}$ y normal $\hat{n}$ a la trayectoria de la partícula. Además, determine el valor del radio de curvatura $\rho_c$ para todo tiempo
Con ayuda de los resultados obtenidos en la parte 3., dibuje la trayectoria entre $t=0$ y $t=\pi/\omega_0$

Hints P1

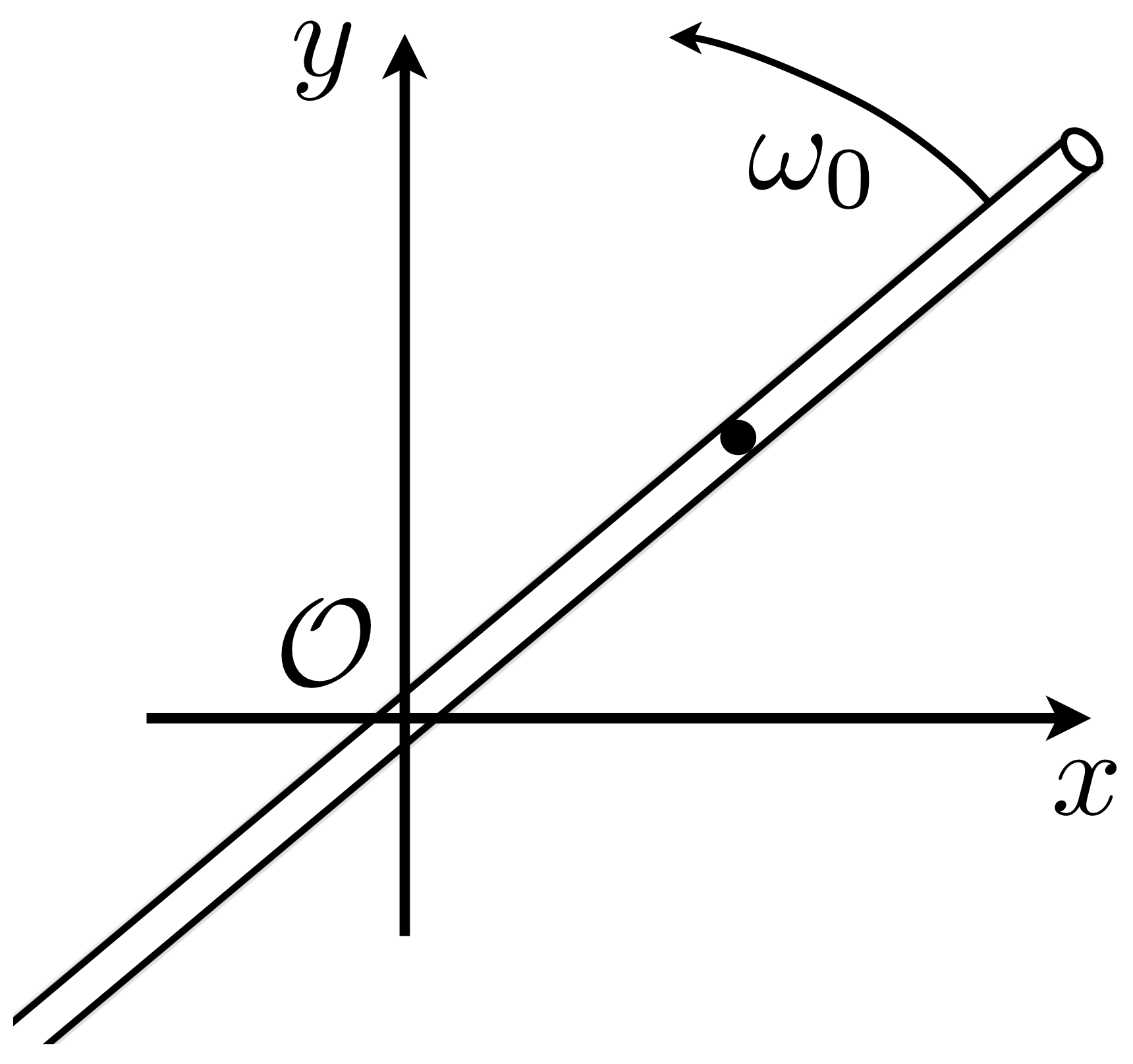
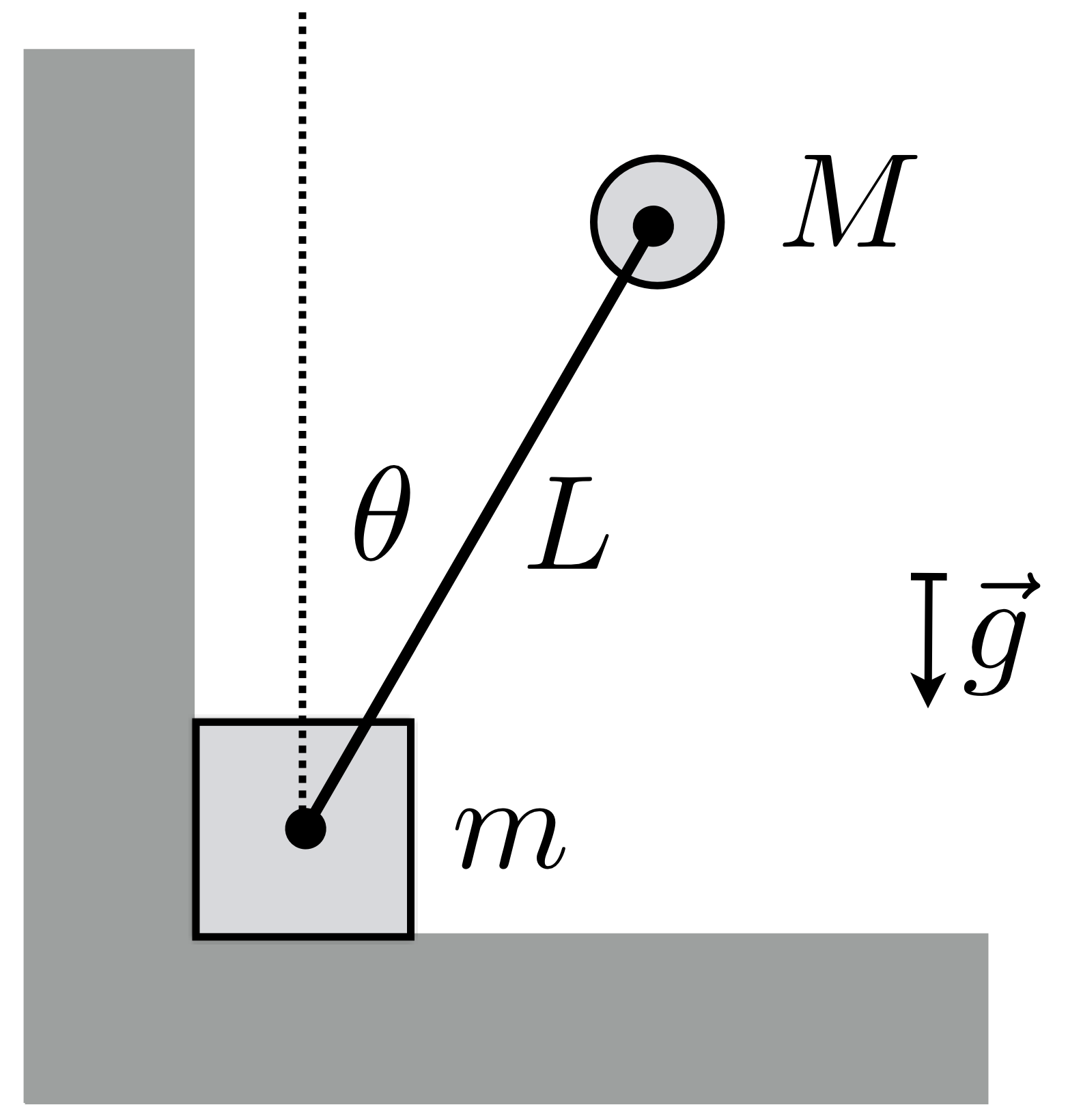
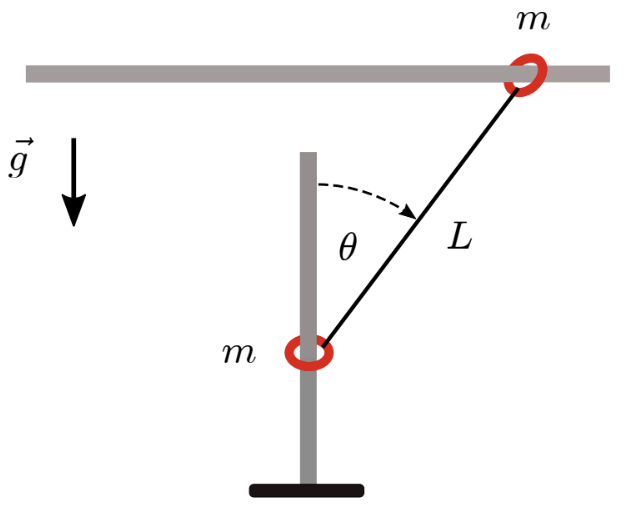
Para 1. recuerden que la posición en polares está dada por:

\begin{equation*} \vec{r}=\rho\hat{\rho}\,. \end{equation*}

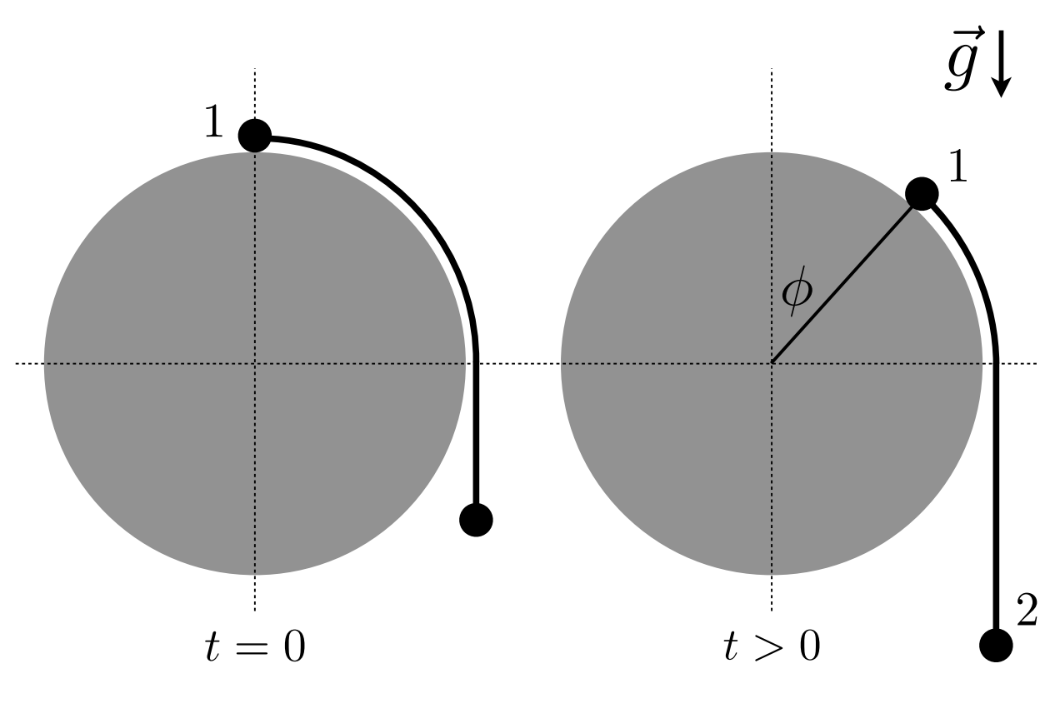
Conocen $\rho$ y pueden calcular $\phi(t)$, así que hay que ocupar trigonometría para descomponer $\hat{\rho}$ (recomiendo no ocupar la fórmula del Formulario 1, háganlo por su cuenta)

También podrían no ocupar polares y encontrar $\vec{r}$ en cartesianas usando trigonometría. Es básicamente lo mismo.
Para 2. tienen que ocupar las expresiones de la velocidad y aceleración en polares y reemplazar con $\rho(t)$ y $\phi(t)$ de este problema.
\begin{equation*} \begin{aligned} \vec{v}&=\,\dot{\rho}\hat\rho + \rho\dot{\phi}\hat\phi\\ \vec{a}&= \left(\ddot{\rho}-\rho\dot{\phi}^2\right)\hat\rho+\left(2\dot{\rho}\dot{\phi}+\rho\ddot{\phi}\right)\hat{\phi} \end{aligned} \end{equation*}
Por 1. ya tienen $\hat\rho$ en función de $\hat{x}$ y $\hat{y}$, hay que hacer algo muy similar con $\hat\phi$

Lo otro que pueden hacer es usar la expresión de $\vec{r}$ en cartesianas y derivar c/r al tiempo y así conseguir la velocidad y aceleración, sin tener que usar las fórmulas.
Para 3., el vector tangente unitario está dado por:

\begin{equation*} \hat{t}=\frac{\vec{v}}{\nu}\,. \end{equation*}

Y, por definición, la derivada temporal del vector tangente, $\dot{\hat{t}}$, es proporcional al vector normal unitario, $\hat{n}$. Usen esto y la definición de vector unitario para encontrar la expresión final de $\hat{n}$
Pueden ocupar la fórmula usual del radio de curvatura u ocupar la relación

\begin{equation*} \dot{\hat{t}}=\frac{\nu}{\rho_c}\hat{n} \end{equation*}

y encontrar $\rho_c$ según la derivada que hicieron antes, $\dot{\hat{t}}$

Una barra rígida de largo $a$ se mueve apoyada en dos paredes rígidas que forman un ángulo recto entre ellas. Suponga que el ángulo $\theta$ es una función arbitrara del tiempo ($\theta = \theta(t)$).

Las siguientes preguntas son para el punto medio de la barra:

Determine el vector posición $\vec{r}$.
Determine el vector velocidad y aceleración.
Encuentre los vectores tangencial $\hat{t}$ y normal $\hat{n}$ a la trayectoria de la partícula.
Exprese la aceleración en esta base de coordenadas.

Hints P2

Utilizar coordenadas cilíndricas para describir la posición del centro
Derivar las expresiones recordando la regla de la cadena
Sabemos que:

\begin{equation*} \hat{t} = \frac{\vec{v}}{v}\,;\qquad \hat{n} = \left|\left| \frac{d\hat{t}}{dt} \right|\right| ^{-1} \frac{d\hat{t}}{dt} \end{equation*}
Sabemos que:

\begin{equation*} \vec{a} = \dot{v}\hat{t} + \frac{v^2}{\rho_c}\hat{n} \end{equation*}

Se tiene una plataforma de largo $L$, que rota con respecto a un eje en el punto $O$, en el extremo izquierdo de la base de largo $2L$, con velocidad angular constante $\dot{\theta}=\omega_0$ como se observa en la Figura.

Una partícula de masa $m$ se encuentra sobre esta plataforma y amarrada a una cuerda de largo $2L$ sujeta al extremo $P$ de la base, o sea, cuando la plataforma comienza a elevarse, $\theta=0$, la cuerda está completamente estirada y la masa se encuentra en el punto $O$, pero con el movimiento de la plataforma comienza a deslizarse sobre ella.

Calcule la distancia de la masa $m$ al origen $O$ en función del tiempo y con esto calcule su posición, velocidad y aceleración en función del ángulo de la plataforma $\theta$.

Hints P3

Definan la longitud de $AP$ como $d$ y ocupe teorema del coseno

\begin{equation*} a^2=b^2+c^2-2bc\cos(\alpha) \end{equation*}

para encontrar una expresión de $d$ en función del largo $L$
Defina la distancia desde $A$ a la masa $m$ como $x$ y la distancia de $O$ a $m$ como $r$ (la distancia solicitada).

Encuentre una relación entre $r$, $L$ y $x$. Use esto y lo del Hint anterior para encontrar una expresión de $r$ en función de $\theta$, o sea $r(\theta)$
Ya con la expresión de $r(\theta)$ encontrada, para calcular la velocidad, $\dot{r}(\theta)$, solo hay que derivar esta expresión con respecto al tiempo.

Y para calcular la aceleración, $\ddot{r}(\theta)$, tienen que derivar otra vez

Parte 2: Dinámica

Una partícula de masa $m$ (partícula 1) puede deslizar sin roce sobre la superficie de un cilindro de radio $R$. Una segunda partícula de igual masa (partícula 2) permanece atada a 1 mediante una cuerda ideal de largo $L>\pi R /2$. Inicialmente ($t=0$) las partículas están en reposo, con 1 en la parte más alta del cilindro (ver figura).

Escriba expresiones para las fuerzas que actúan sobre ambas partículas.
Obtenga la ecuación de movimiento para el ángulo $\phi$ que describe la posición de la partícula 1.
Integre la ecuación obtenida en la parte anterior, para obtener $\dot{\phi}$ en función de $\phi$.
Obtenga una ecuación que permita determinar el ángulo en el cuál la partícula 1 se despega del cilindro.

Hints P4

Considerar la normal, gravedad y tensión para la partícula 1, y gravedad y tensión para la partícula 2
La partícula 1 solo se mueve a lo largo del círculo, mientras que la 2 solo se mueve verticalmente. Por lo que es conveniente ocupar coordenadas polares para la masa 1 y cartesianas para la masa 2
Para obtener la EoM de $\phi$ necesitan hacer segunda Ley de Newton para la masa 1
\begin{equation*} m\vec{a}_1=\sum_i \vec{F}_{1,i}\,. \end{equation*}

Notarán que en la ec. escalar con $\ddot{\phi}$ aparece la tensión $T$, que es una incógnita. Por lo que también deben encontrar la EoM de la masa 2 para encontrar una expresión de $T$ y reemplazarla en la EoM de $\phi$
Si hicieron el paso anterior, debieron haber encontrado algo como

\begin{equation*} mR\ddot{\phi}=-m\ddot{z}+\dotsb\,. \end{equation*}

Así que deben encontrar una relación geométrica entre $\phi$ y $z$, para así encontrar una relación entre $\ddot{\phi}$ y $\ddot{z}$ y finalmente encontrar una ecuación de la forma:

\begin{equation*} \ddot{\phi}=f(\phi) \end{equation*}
Para integrar la EoM encontrada, deben recordar que $2\dot{\phi}\ddot{\phi} = \frac{d}{dt}\dot{\phi}^2$ o también puede ocupar el trucazo de mecánica

\begin{equation*} \ddot{\phi}=\dot{\phi}\frac{\textnormal{d}\dot{\phi}}{\textnormal{d}\phi} \end{equation*}
Cuando la partícula se despega, la normal se hace 0

Considere una partícula de masa $m$ que puede deslizar sin roce sobre un cascarón semi-esférico hueco de radio $R$. La partícula se encuentra atada a una cuerda ideal que penetra hacia el interior del cascarón por su punto más alto $P$, como muestra la figura.

Si el extremo $Q$ de la cuerda se mantiene fijo tal que el ángulo cenital de la partícula se mantiene siempre en $\theta=60^\circ$, determine la máxima rapidez $v_0$ que la partícula puede tener, tal que ella describa un movimiento circular uniforme en torno al eje $\mathcal{O}P$ sin separarse del cascarón
Si la partícula tiene inicialmente una rapidez acimutal $v_1$, menor al valor determinado en 1., y el extremo $Q$ de la cuerda es tirado hacia abajo con rapidez $v_Q$, encuentre una expresión para la fuerza normal que el cascarón ejerce sobre la partícula en función de su ángulo cenital $\theta$

Hints P5

Por la forma del cascarón, y por lo tanto del movimiento de la partícula, es claro que hay que ocupar coordenadas esféricas
Por la restricciones mencionadas en 1. tendríamos:

\begin{equation*} r=R\,,\qquad \theta=\frac{\pi}{3} \end{equation*}

así que sus derivadas son nulas

\begin{equation*} \dot{r}=\ddot{r}=0\,,\qquad \dot{\theta}=\ddot\theta=0\,, \end{equation*}

mientras que $\dot{\phi}$ es constante y en función de $v_0$ y $R$
Las fuerzas actuando sobre la partícula son:
- Gravitacional
- Normal
- Tensión
Deben expresarlas en el sistema de coordenadas elegido. Solo la fuerza gravitacional tiene una expresión conocida de antes: $\vec{F}_P=-mg\hat{k}$, la normal y la tensión no se conocen a priori
Con segunda Ley de Newton, $m\vec{a}=\sum_i\vec{F}$, consiguen la ecuación de movimiento vectorial. Con esto pueden obtener las ecuaciones de movimiento escalares
Para encontrar la condición solicitada en 1. hay que usar la EoM escalar que contenga la normal $N$ y esta igualarla a 0, $N=0$. De aquí se despeja $v_0$
En 2. ya no se tiene $\dot\theta=0$, sino que esta rapidez está en función de $v_Q$ y $R$. Hacen segunda Ley de Newton nuevamente y una de las EoM escalares contendrá la expresión de la fuerza normal

Considere un bloque de masa $m$ colocado sobre una superficie horizontal y apoyado sobre una pared vertical. El bloque sirve de apoyo para una barra, de modo que esta pueda girar libremente en un plano vertical (ver figura). En el otro extremo de la barra (de largo $L$ y masa despreciable) se fija una partícula de masa $M = 2m$. Todos los roces son despreciables. Inicialmente la barra se encuentra en posición vertical, y debido a un pequeño impulso, se desestabiliza y comienza a girar.

Deduzca una ecuación de movimiento para $\theta$
A partir del resultado anterior, demuestre que $\dot\theta$ y $\theta$ satisfacen la relación ${\dot\theta}^2=2(g/L)(1-\cos\theta)$
Determine las fuerza normales que la superficie horizontal y la pared, ejercen sobre el bloque ($N_h$ y $N_p$, respectivamente), en función del ángulo $\theta$, mientras que este no se desplaza
Indique que sucede primero: el bloque se levanta de la superficie horizontal o el bloque se despega de la pared. ¿Para qué ángulo crítico $\theta_*$ ocurre esto?

Hints P6

Aunque en la pregunta 4. se menciona que la masa de la esquina se puede separar de las paredes, en todo el movimiento esta se mantiene quieta. Un movimiento posterior a que se separe de la parede, no es de nuestro interés en este caso.
Por el movimiento de $M$, una circunferencia de radio $L$, para esta partícula es recomendable ocupar coordenadas polares en el plano del movimiento.
Las fuerzas actuando directamente sobre $M$ son:
- Gravitacional
- Normal de la barra
donde la normal ejercida por la barra es en la misma dirección de esta, en $\hat\rho$. Con esto y segunda Ley de Newton encontramos las ecuaciones de movimiento
Una de las EoM escalares sería de la forma

\begin{equation*} \ddot\theta=\ddot\theta(\theta) \end{equation*}

por lo que para integrarla debemos ocupar el trucazo de mecánica

\begin{equation*} \ddot\theta=\dot\theta\frac{\textnormal{d}\dot\theta}{\textnormal{d}\theta}\,. \end{equation*}

Con esto deberían conseguir una expresión como $\dot\theta=\dot\theta(\theta)$ como se solicita
Para encontrar las fuerzas normales ejercidas por las paredes sobre $m$ es conveniente ocupar coordenadas cartesianas, tomando aceleración nula ($\vec{a}_M=\vec{0}$) y considerando que las fuerzas que actuan sobre esta son:
- Gravitacional
- Normal de la barra
- Normal del piso
- Normal de la pared izquierda
Para ver desde dónde se despega primero $m$ hay que analizar las EoM que contienen a $N_h$ y $N_p$. Se despegará de la pared cuya fuerza normal cambie primero de signo

Sobre dos barras, una horizontal y otra vertical, deslizan sin roce dos anillos de masa $m$ cada uno, unidos por una cuerda ideal de largo $L$. Considerando que el sistema se libera desde el reposo, cuando la cuerda forma un ángulo $\theta_0$ con la vertical, determine:

La ecuación de movimiento para el ángulo $\theta$
Las velocidades de ambos anillos
La tensión de la cuerda

Hints P7

Por el movimiento del sistema, no utilizar sistema de coordenadas cilíndricas, puesto que sería no inercial y también afectaría a la definición del ángulo $\theta$

Por lo que podemos ocupar el siempre confiable sistema de coordenadas cartesiano, para ambas partículas. Con este sistema escriba las EoMs de ambas masas.
Como piden la EoM de $\theta$, usando trigonometría tienen que escribir en función de $\theta$ las posiciones en cartesianas.

Por ejemplo, la posición de la partícula de arriba quedaría como

\begin{equation*} x_1=L\sin\theta \end{equation*}

así que su aceleración sería:

\begin{equation*} \ddot{x}_1=-L\dot{\theta}^2\sin\theta+L\ddot{\theta}\cos{\theta} \end{equation*}
Junte las EoMs de ambas partículas para eliminar la tensión
Ya con la EoM de $\theta$ de la forma

\begin{equation*} \ddot{\theta}=f(\theta) \end{equation*}

para integrar ocupen truco de mecánica

\begin{equation*} \ddot{\theta}=\dot\theta\frac{\textnormal{d}\dot{\theta}}{\textnormal{d}\theta} \end{equation*}