Mecánica FI2001

Sesión 2

Parte 1: Energía, trabajo y pequeñas oscilaciones

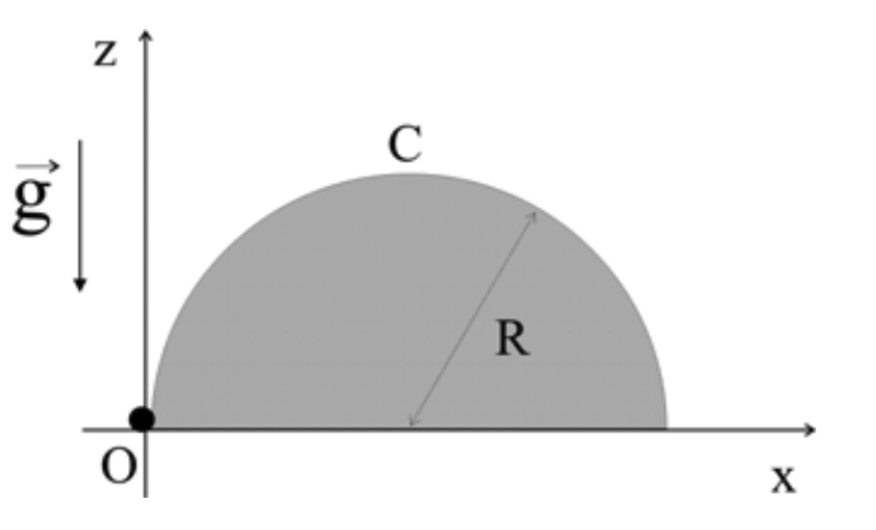
Una partícula de masa $m$ se mueve con rapidez constante $v_0$ por el exterior de un semicilindro horizontal de radio $R$. Además del peso y la fuerza normal que ejerce la superficie, la partícula está sometida a otras dos fuerzas. La primera es una fuerza $\vec{F}_1$ que está descrita por la expresión:

\begin{equation*} \vec{F}_1=-c\left(xz^2\hat{i} + zx^2\hat{k}\right) \end{equation*}

donde $c$ es una constante conocida y las coordenadas $x$ y $z$ se miden con respecto al origen O. La otra fuerza $\vec{F}_2$, para la cual no se cuenta con una expresión explícita, es la que permite que la partícula se mueva con rapidez constante es su trayectoria desde el origen O a la cúspide C. Se pide:

Mostrar que la fuerza $\vec{F}_1$ es conservativa
Determinar una expresión para el potencial asociado $\vec{F}_1$
Determinar el trabajo efectuado por la fuerza $\vec{F}_2$ en el trayecto O a C

Hints P1

Para 1. calcular el rotor de la fuerza usando coordenadas cartesianas
Para 2., usar que el potencial cumple $\vec{F}_1 = -\nabla U$, que ocupando coordenadas cartesianas tendríamos:

\begin{equation*} \frac{\partial U(x,z)}{\partial x}=-F_x=cxz^2 \Rightarrow U(x,z) = c\frac{x^2z^2}{2} + c_1(z), \end{equation*}

y luego deben encontrar la dependencia de la constante de integración $c_1(z)$ utilizando la otra relación:

\begin{equation*} \frac{\partial U(x,z)}{\partial z}=-F_z=czx^2 \end{equation*}
Para 3. recordar que para las fuerzas conservativas, su trabajo se puede calcular como $W_{A\to B}^{\textnormal{C}}=U(\vec{r}_A)-U(\vec{r}_B)$
El trabajo total (considerando tanto fuerzas conservativas como no conservativas) es igual a $W^{\textnormal{tot}}_{A\to B}=K(\vec{r}_B)-K(\vec{r}_A)$

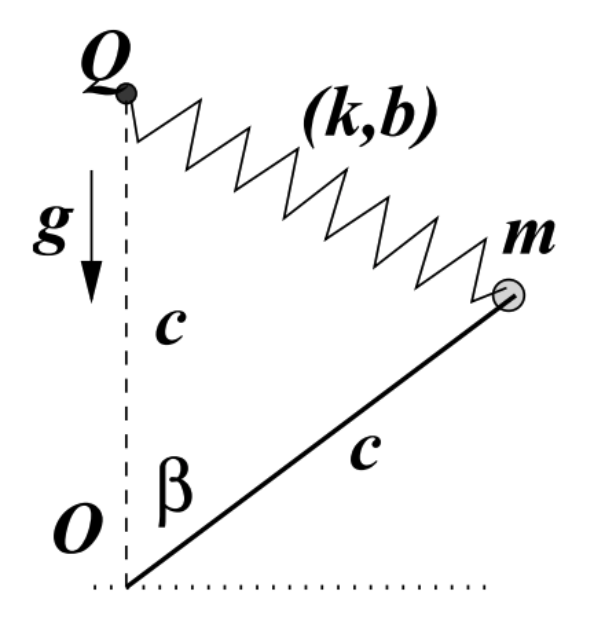
Una vara ideal de masa despreciable y largo $c$ puede girar en un plano vertical en torno a un punto $O$. En su extremo libre tiene una masa puntual $m$, masa que a su vez está unida a un resorte de largo natural $b$ y constante elástica $k$. El otro extremo del resorte está fijo a un punto $Q$ que está a distancia $c$ sobre $O$.

Escriba la energía mecánica total del sistema
Obtenga el valor que debe tener la masa $m$ para que $\beta=\pi/3$ sea un punto de equilibrio
Para este último caso, y con $c=2b$ obtenga la frecuencia de pequeñas oscilaciones del sistema

Hints P2

Para 1. solo se tiene la fuerza gravitatoria y la elástica, ustedes conocen las expresiones de sus energías potenciales
Para 2. los puntos de equilibrio están dados por $\frac{\partial U_{tot}(\phi)}{\partial \phi}=0$ en $\phi = \phi_{eq}$
Para 3. tiene que tener ojo ya que la energía quedaría como $E=\frac{1}{2}\alpha\dot{\phi}^2+U_{tot}(\phi)$. Deben encontrar identificar la expresión del $\alpha$
La frecuencia de pequeñas oscilaciones (para este tipo de energías) es $\omega=\sqrt{U_{tot}''(\phi_{eq})/\alpha}$

Considere una partícula de masa $m$ que se mueve en un campo de fuerza de atracción central $\vec{F}=-c\hat{r}$, donde $c$ es una constante positiva (note que la magnitud de la fuerza es constante).

Demuestre que la partícula no puede escapar de este campo de atracción
Si se verifica que la partícula se encuentra en una órbita circular de radio $r = r_0$, determine el periodo de pequeñas oscilaciones que experimenta la distancia entre la partícula y el centro de atracción cuando la partícula sufre una pequeña perturbación radial.
Suponga que la partícula se encuentra en la órbita circunferencial de la parte b) y, como resultado de un impulso radial, en dirección opuesta al centro de atracción, la partícula queda en una órbita tal que su distancia máxima al centro de atracción es $2r_0$. Determine cuánto aumenta la energía mecánica total de la partícula como resultado de este impulso.

Hints P3

Calcule la energía potencial asociada a la fuerza $\vec{F}$ ¿se puede sobrepasar esta energía con una energía inicial finita?
Para 2., se conserva el momentum angular, por lo que hay que sumarle un término (que viene de la energía cinética) a la energía potencial calculada en 1.
Por si el Hint anterior no fue suficiente, la energía quedaría como

\begin{equation*} \begin{aligned} E&=\frac{1}{2}m\dot{\rho}^2+f(\rho)+U(\rho)\\ &=\frac{1}{2}m\dot{\rho}^2+U_{eff}(\rho) \end{aligned} \end{equation*}

Encuentre la expresión de $f(\rho)$ y derive dos veces $U_{eff}(\rho)$ para encontrar la frecuencia de pequeñas oscilaciones
Para 3. usted puede calcular la energía inicial. Para la energía final, tiene que considerar que $\dot\rho_f=0$ cuando se llega a $\rho=2r_0$ y puede calcular $\dot{\phi}$ por conservación del momentum angular

Parte 2: Torque y momentum angular

[Recomiendo saltarse esta pregunta] o ver la pauta en: este link.

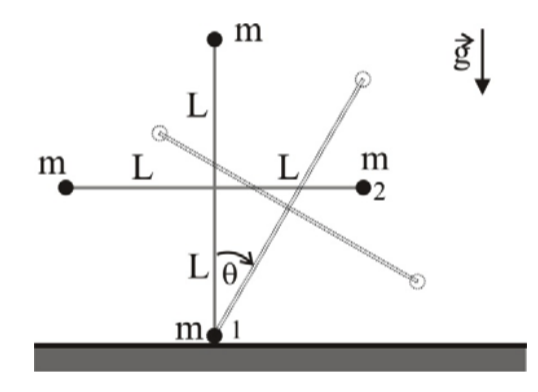
Considere una estructura rígida formada por dos varas sin masa de largo $2L$ que forman una cruz simétrica como muestra la figura. En los extremos de las varas se ubican 4 partículas puntuales de masa $m$ cada una. Si inicialmente la estructura se encuentra en reposo en su posición de equilibrio inestable ($\theta=0^{\circ}$) y se le da una pequeña perturbación que la hace volcar como se indica, se pide:

Calcule el valor de $\dot\theta$ para el instante justo antes de que la partícula 2 choca con la superficie (asuma que hasta antes del choque la partícula 1 no se mueve)
Encuentre una expresión de la normal ejercida en 1 justo antes de que la partícula 2 choca con la superficie, en función de $\dot\theta$ y $\ddot\theta$
Para calcular la normal de 2.

Calcule el momentum angular total del sistema
Calcule el torque total del sistema
Encuentre la ecuación de movimiento para $\theta$

Hints P4

Para 1), utilice conservación de la energía mecánica considerando $E_0$ en el momento inicial y $E_f$ justo antes de que 2 toque el piso. La única energía potencial es la gravitacional
Para 2), ocupe la Segunda Ley de Newton para un sistema de partículas

\begin{equation*} M_{\textnormal{tot}}\ddot{\vec{R}}_{\textnormal{CM}}=\sum_i \vec{F}_i^{\textnormal{ext}} \end{equation*}
Luego de ocupar la Segunda Ley de Newton para un sistema de partículas, exprese la altura del centro de masa en función del ángulo $\theta$, $\vec{R}_{\textnormal{CM}}=\vec{R}_{\textnormal{CM}}(\theta)$ y derívelo dos veces para obtener la aceleración
Para 3), considere que las 3 partículas en movimiento siguen circunferencias, por lo que sus velocidades son de la forma $\vec{v}_i=L_i\dot\phi_i\hat{\phi}_i$
Para 3), va a tener que ocupar un sistema de coord. cilíndrico distinto para cada partícula (distinto $\hat{\rho}_i$ y $\hat{\phi}_i$), pero eso no importa cuando calculamos el momentum angular o el torque, ya que todos los productos cruz darán en la dirección de $\hat{k}$, que es el mismo para el sistema de todas las partículas

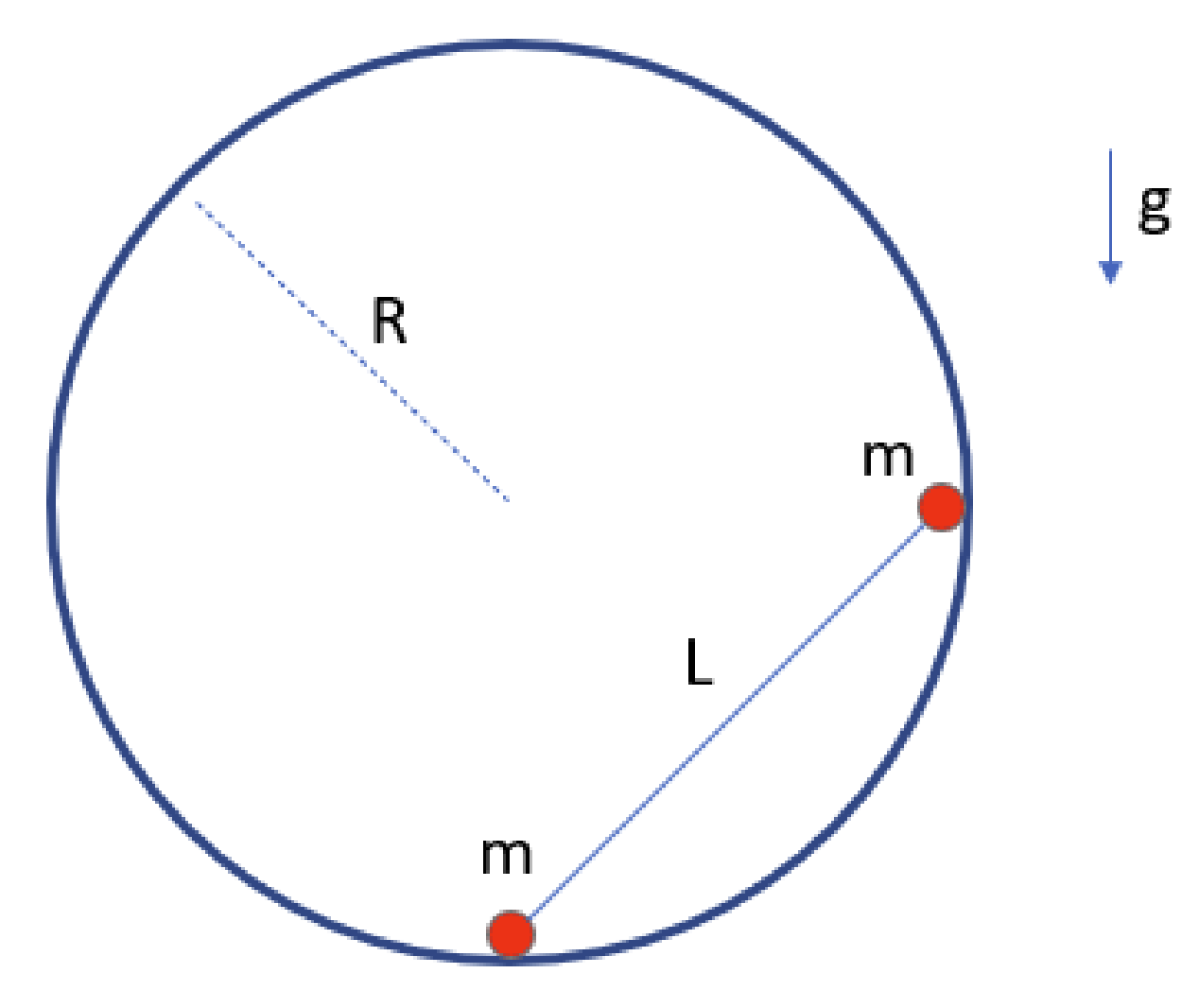
Considere un cilindro hueco de radio $R$, colocado en posición horizontal. En el interior del cilindro se encuentran dos partículas de masa $m$ cada una, unidas por una barra de largo $L = \sqrt{2}R$, colocadas en un plano perpendicular al eje del cilindro, con una de las dos partículas ubicada en el punto más bajo del cilindro (ver figura adjunta). En algún momento la barra se suelta desde el reposo, en esa posición. Determine:

Rapidez de las partículas cuando la barra pasa por la posición horizontal
Magnitud de la aceleración de las partículas cuando la barra pasa por la posición horizontal
Calcule el periodo de pequeñas oscilaciones que ocurren si estando la barra en reposo en posición horizontal se la perturba ligeramente, sacándola desde esa posición

Hints P5

Para 1. puede utilizar conservación de la energía mecánica para obtener la expresión de $\dot\phi$ en función del ángulo $\phi$ (ángulo entre la vertical y la posición de las partículas) o puede encontrar la ecuación de movimiento de $\phi$ (y luego integrarla una vez) usando la ecuación maestra

\begin{equation*} \vec{\tau}_{\textnormal{tot}}=\frac{d \vec{L}_{\textnormal{tot}}}{dt}\,, \end{equation*}

donde si usamos como origen el centro de la circunferencia, las normales no ejercen torque
Para 2. sabe que la magnitud de la aceleración en cilíndricas, para este problema, es:

\begin{equation*} |\vec{a}|=\Big|-R\dot{\phi}^2\hat\rho + R\ddot\phi\hat\phi\Big| \end{equation*}
Para 3), note que la energía mecánica le queda como $E=\frac{1}{2}\alpha \dot{\phi}^2 + U_{\textnormal{tot}}(\phi)$, por lo que la frecuencia se calcula como:

\begin{equation*} \omega=\sqrt{\frac{\left.U_{\textnormal{tot}}''(\phi)\right|_{\phi=\phi_{\textnormal{eq}}}}{\alpha}} \end{equation*}

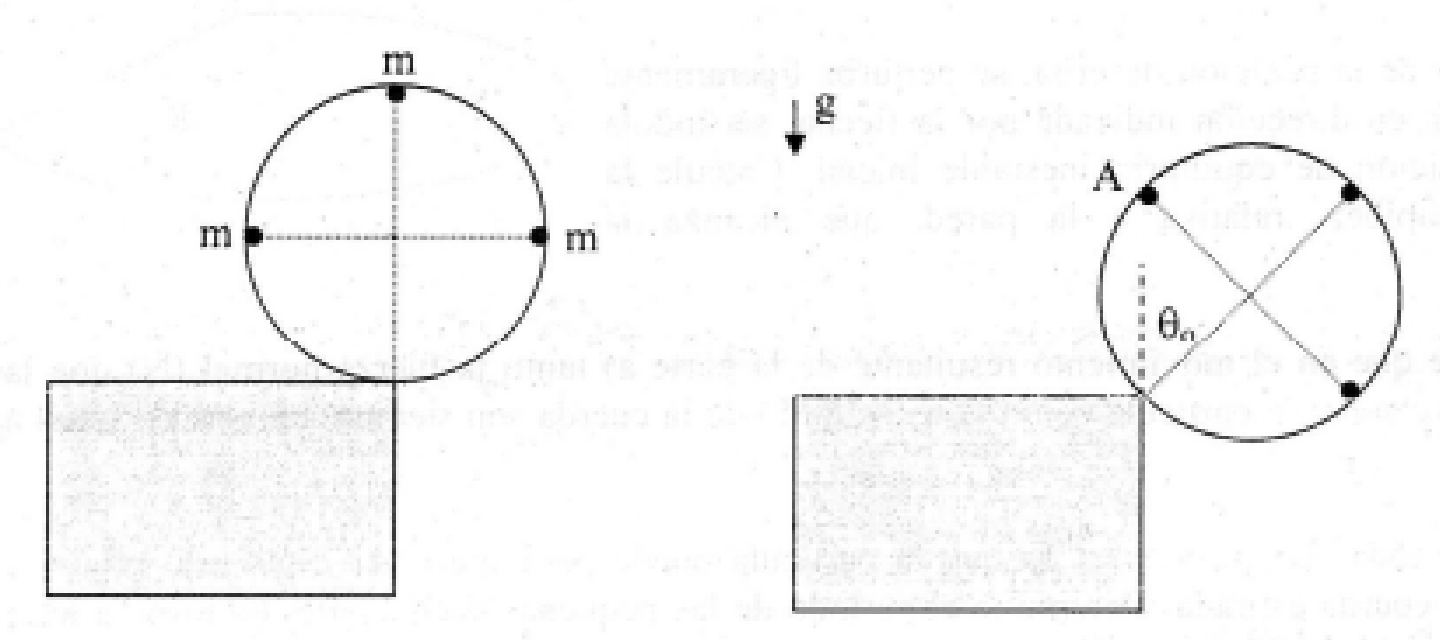
Considere un disco de radio $R$ y masa despreciable que se encuentra apoyado en el borde de una superficie horizontal. Sobre el disco, y pegadas a él, se encuentran 3 partículas de masa $m$ cada una, dispuestas en la forma indicada en la figura adjunta. En un cierto momento la estructura se desestabiliza a partir del resposo y empieza a caer

Suponiendo que cuando el disco ha girado un ángulo $\theta_0$ todavía no desliza ni se despega del borde, calcule la magnitud de la fuerza normal y la fuerza de roce que se ejerce sobre el disco en la zona de contacto con la superficie horizontal, en función del ángulo $\theta_0$. Suponiendo que el ángulo $\theta_0=\pi/4$, determine la magnitud de la fuerza de adhesión entre la partíucla A y el disco en esta posición.

Hints P6

Utilice un sistema de coordenadas cilíndrico con origen en el borde de la superficie horizontal
Para encontrar expresiones (en función del ángulo y sus derivadas) de las fuerzas que actúan sobre el disco (la normal y el roce), ocupe la Segunda Ley de Newton para un sistema de partículas

\begin{equation*} M_{\textnormal{tot}}\ddot{\vec{R}}_{\textnormal{CM}}=\sum_i \vec{F}_i^{\textnormal{ext}} \end{equation*}
Para calcular $\dot\theta$ y $\ddot\theta$ en función del ángulo, encuentre la ecuación de movimiento de $\theta$ usando la ecuación maestra

\begin{equation*} \vec{\tau}_{\textnormal{tot}}^{ext}=\frac{d \vec{L}_{\textnormal{tot}}}{dt}\,, \end{equation*}
Para calcular la fuerza de adhesión entre la partícula A y el disco, defina su posición como

\begin{equation*} \vec{r}_A=R\hat\rho-R\hat\theta\,, \end{equation*}

derive dos veces esta expresión para obtener la aceleración y ocupe Segunda Ley de Newton para esta partícula en particular
La ecuación de movimiento vectorial para la partícula A sería como

\begin{equation*} m\ddot{\vec{r}}_A=f_{\textnormal{ad},\rho}\hat\rho +f_{\textnormal{ad},\theta}\hat\theta + m\vec{g} \end{equation*}

donde la fuerza de adhesión se expresó como $\vec{f}_{\textnormal{ad}}=f_{\textnormal{ad},\rho}\hat\rho +f_{\textnormal{ad},\theta}\hat\theta$