Antecedentes

Un vórtice es una estructura fluida, normalmente en rotación, que posee vorticidad. Un remolino en el agua de bañera, un tornado atmosférico o la rotación del polvo estelar de una galaxia en formación, son algunos de los ejemplos donde observamos estas estructuras.

Conceptos

El concepto matemático clave es la vorticidad, que define la cantidad de circulación o rotación que posee un vórtice. La vorticidad ( $\mathbf{\omega}$) se define como el rotor del campo de velocidad ( $\mathbf{u}$), por lo tanto es un vector alineado con el eje rotación del vórtice.

$$\mathbf{\omega} = \nabla \times \mathbf{u}$$

La intesidad de la rotación del vórtice se mide a través de la circulación $\Gamma$ del campo de velocidad. Si el vórtice es puntual, es decir toda su vorticidad está concentrada en un punto, y además la única componente de la velocidad es $\mathbf{u} = u \hat \theta$, entonces la velocidad estará dada por

$$\mathbf{u} = \frac{\Gamma}{2\pi r} \hat{\theta} \qquad \textrm{donde la circulaci\'on es}\qquad \Gamma = \oint \mathbf{u}\cdot d\mathbf{l}$$

Figura: Concepto de vórtice y su campo de velocidad

En la figura 1 se muestra el concepto de vórtice así como la dependencia de la velocidad $u_\theta(r)$ en función de la distancia al centro del vórtice $r$. Este es un caso ideal, ya que la aparente divergencia entorno a $r=0$ no ocurre en práctica, porque la vorticidad no se encuentra concentrada en un punto material, sino que en una zona de tamaño finito.

Figura: Concepto de vórtice tipo tornado donde se aprecia que es una estructura 3D. Si hay nubes, estas son movidas por el campo de velocidad del vórtice y entonces se puede apreciar su estructura.

Un vórtice puede generarse debido a condiciones particulares del flujo, como es el caso de los vórtices atmosféricos. La estructura se pone en rotación rápida y puede alcanzar velocidades muy importantes. Se pueden hacer visibles cuando atrapan nubes o polvo a su paso, como se aprecia en la figura 2.

A la escala de laboratorio, los vórtices se pueden crear simplemente al interponer un obstáculo rígido en un flujo uniforme. El caso más conocido y documentado es la creación de vórtices aguas abajo de un cuerpo cilíndrico [3].

La calle de vórtices de von Kármán se desarrolla cuando el número de Reynolds del flujo $Re = \rho U_0 d/\mu$ alcanza el valor $Re \sim 50$ (Para el aire a 15 C, $\mu=1.78\times 10^{-5}$ [Kg$/$ms] y $\rho = 1.22$ [Kg$/$m$^3$]). Si el número de Reynolds es sub-crítico, $1 < Re < 50$, 2 torbellinos simétricos se forman en la parte posterior del cuerpo y se mantienen adosados girando en sentido contrario, pero sin ser emitidos aguas abajo del cuerpo.

Sin embargo, si el flujo se vuelve super-crítico para $Re > 50$, estos torbellinos comienzan a oscilar transversalmente, terminando por desprenderse en forma alternada. Se trata de una inestabilidad del flujo donde el parámetro crítico es el número de Reynolds.

Aquí observamos vórtices alternados generados aguas abajo de un cuerpo circular [1]. Si la velocidad del flujo es suficientemente alta, éstos son emitidos y advectados por el flujo, creando entonces la famosa calle de vórtices de von Kármán o Kármán vortex street[2]. La calle de vórtices de von Kármán aparece y se desarrolla cuando el número de Reynolds del flujo $Re = \rho U_0 d/\mu$ alcanza el valor $Re \sim 50$ (Para el aire a 15 C, $\mu=1.78\times 10^{-5}$ [Kg$/$ms] y $\rho = 1.22$ [Kg$/$m$^3$]). El orden espacio-temporal de la calle de vórtices prevalece hasta $Re \sim 150$.

Vórtices de Kármán - de la Tierra al Laboratorio

Observaciones a gran escala se repiten en laboratorio. Para los vórtices de Kármán existen 4 parámetros típicos que originan 2 números sin dimensión que representan físicamente esas estructuras.

Isla Robinson Crusoe $\;\;\;\;\;\;\;\;\;\;\;$ Flujo sobre cilindro $\;\;\;\;\;\;\;\;\;\;\;\;\;$ Burbuja en agua

Parámetros sin dimensión

El número de Reynolds se obtiene como la razón entre fuerzas inerciales y viscosas y el número de Roshko se obtiene como la razón entre tiempos:

$$\textrm{Reynolds} \longrightarrow \qquad Re = \frac{\rho U_0 d}{\mu}$$

$$\textrm{Roshko} \longrightarrow \qquad Ro = \frac{fd^2}{\nu}$$

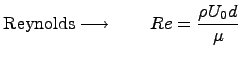
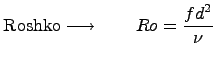
Donde un aspecto importante es la frecuencia de desprendimiento de los vórtices $f$ [Hz] en el caso que el cuerpo es un cilindro de diámetro $d$. Experimentos realizados en la década de 50 [3] probaron que la frecuencia $f$ aumentaba con la velocidad del flujo $U_0$. Sin embargo, si $U_0$ se mantenía constante, $f$ disminuía si se incrementaba el diámetro del cilindro. Sorprendentemente la ley experimental se vuelve una función lineal cuando se presenta en forma adimensional, usando el número de Reynolds y el número de Roshko.

$${fd^2/\nu \sim a Re + b} \qquad \textrm{con} \qquad a=0.212 \;\textrm{y}\; b = -4.5 \qquad \textrm{para}\qquad 50<Re<150$$ (1)

Donde $\;\nu \;$es la viscosidad cinemática, $\;\nu = \mu/\rho \;$[m$^2/$s].

Dicha frecuencia temporal determina una cierta periodicidad espacial $\lambda$ entre los vórtices de igual signo.

Figura: Detalles de la calle de von Kármán. Los vórtices superiores giran en sentido de las manecillas del reloj, mientras que los de abajo, giran en sentido contrario.

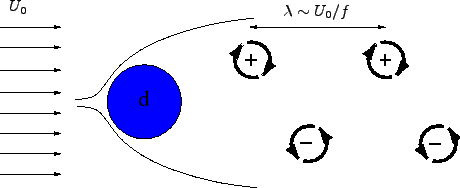Cálculo Si consideramos que el número de Reynolds crítico es $Re_c=50$, para un cilindro de diámetro $d=0.5$ [cm] sumergido en un flujo de aire con viscosidad cinemática $\nu=0.15$ [cm$^2/$s], el valor de la velocidad debe ser $U_0 \geq 15$ [cm$/$s] para poder observar la calle de vórtices de von Kármán. La frecuencia de desprendimiento de vórtices $f$ viene dada por la ecuación 1

$$f \sim \frac{\nu}{d^2}\left(a Re +b\right) \qquad f \sim 3.6 \textrm{[Hz]}$$